题目内容
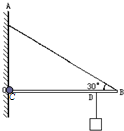
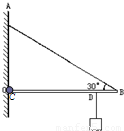
如图所示，水平轻杆CB长1m，轻杆与墙通过转轴O连接．现在离B点20cm处D点挂一重50N的物体，则绳AB中的拉力为 N；O对C的作用力的方向沿 （填“水平”、“斜向上”、“斜向下”）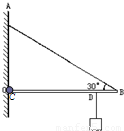
【答案】分析：轻杆处于平衡状态，合力矩为零．以C转轴，根据力矩平衡条件列式，求得绳AB中的拉力．运用正交分解法，根据力平衡条件，分别确定出竖直和水平两个方向分力的方向，即可确定O对C的作用力的方向．
解答：解：则以C转轴，根据力矩平衡条件得
G?LCD=F?LBCsin30°
得绳AB中的拉力F=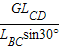
=
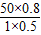N=80N
设O对C的作用力大小为F，水平分力为Fx，竖直分力为Fy．
根据轻杆平衡知：
竖直方向：G=Fsin30°+Fy，则得Fy=G-Fsin30°=50N-80×0.5N=10N，方向竖直向上．
水平方向：Fx=Fcos30°，则得Fx方向水平向右．
所以F的方向为斜向上
故答案为：80，斜向上
点评：本题考查考了杠杆平衡和力平衡条件的应用，正确找出力臂，运用正交分解法研究O对C的作用力的方向是解题的关键．
解答：解：则以C转轴，根据力矩平衡条件得
G?LCD=F?LBCsin30°
得绳AB中的拉力F=
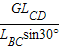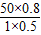=N=80N设O对C的作用力大小为F，水平分力为Fx，竖直分力为Fy．
根据轻杆平衡知：
竖直方向：G=Fsin30°+Fy，则得Fy=G-Fsin30°=50N-80×0.5N=10N，方向竖直向上．
水平方向：Fx=Fcos30°，则得Fx方向水平向右．
所以F的方向为斜向上
故答案为：80，斜向上
点评：本题考查考了杠杆平衡和力平衡条件的应用，正确找出力臂，运用正交分解法研究O对C的作用力的方向是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
（2010?长宁区一模）如图所示，水平轻杆CB长1m，轻杆与墙通过转轴O连接．现在离B点20cm处D点挂一重50N的物体，则绳AB中的拉力为
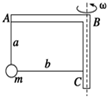质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点，如图所示，当轻杆木架绕轴BC以角速度ω匀速转动时，小球在水平面内做匀速圆周运动，绳a在竖直方向，绳b在水平方向，当小球运动到图示位置时，绳b被烧断的同时木架停止转动，则下列说法中错误的是（ ）| A、小球仍在水平面内做匀速圆周运动 | B、在绳b被烧断瞬间，绳a中张力突然增大 | C、若角速度ω较小，小球在垂直于平面ABC的竖直平面内摆动 | D、若角速度ω较大，小球可在垂直于平面ABC的竖直平面内做圆周运动 |
