题目内容
如图所示，横截面为直角三角形斜劈A，放在粗糙的水平地面上，在劈与竖直墙壁之间放置一光滑球B，系统处于静止状态．在球B上施一通过球心的力F，系统仍保持静止，下列说法正确的是（ ）分析：正确选择研究对象，对其受力分析，运用平衡条件列出平衡等式解题．
解答：解：不加推力时，选取A和B整体为研究对象，它受到重力（M+m）g，地面支持力N，墙壁的弹力F′和地面的摩擦力f的作用（如图所示）而处于平衡状态．
根据平衡条件有：N-（M+m）g=0，F′=f，可得：N=（M+m）g．
再以B为研究对象，它受到重力mg，三棱柱对它的支持力NB，墙壁对它的弹力F的作用（如图所示），而处于平衡状态，根据平衡条件有：
NB cosθ=mg
NsinθB=F′
解得
F′=mgtanθ，
所以
f=F′=mgtanθ ①
加推力F，相当于物体B的重力变大，由于物体仍然平衡，故合力仍然为零，故A错误；
B对竖直墙壁的压力等于墙壁对物体B的支持力F′，加推力F，相当于物体B的重力mg变大，再由①式，得到压力变大，故B正确；
加推力F，相当于物体B的重力mg变大，再由①式，得到摩擦力f变大，故C错误；
加推力F，相当于物体B的重力mg变大，再由①式，A对地面的摩擦力始终等于B对墙壁的压力，故D错误；
故选B．
根据平衡条件有：N-（M+m）g=0，F′=f，可得：N=（M+m）g．
再以B为研究对象，它受到重力mg，三棱柱对它的支持力NB，墙壁对它的弹力F的作用（如图所示），而处于平衡状态，根据平衡条件有：
NB cosθ=mg
NsinθB=F′
解得
F′=mgtanθ，
所以
f=F′=mgtanθ ①
加推力F，相当于物体B的重力变大，由于物体仍然平衡，故合力仍然为零，故A错误；
B对竖直墙壁的压力等于墙壁对物体B的支持力F′，加推力F，相当于物体B的重力mg变大，再由①式，得到压力变大，故B正确；
加推力F，相当于物体B的重力mg变大，再由①式，得到摩擦力f变大，故C错误；
加推力F，相当于物体B的重力mg变大，再由①式，A对地面的摩擦力始终等于B对墙壁的压力，故D错误；
故选B．
点评：正确选择研究对象，对其受力分析，运用平衡条件列出平衡等式解题．要注意多个物体在一起时，研究对象的选取．
练习册系列答案
相关题目
电磁流量计广泛应用于测量可导电流体（如污水）在管中的流量（在单位时间内通过管内横截面的流体的体积）．为了简化，假设流量计是如图所示的横截面为长方形的一段管道，长、宽、高分别为图中的a、b、c表示，左右两端开口，流量计的两端与输送流体的管道相连接．图中流量计的前后两面是金属材料，上下两面是绝缘材料．现于流量计所在处加竖直向下磁感应强度为B的匀强磁场，在管外将流量计前后两表面用导线串接一电阻R和电流表，当流体匀速流经流量计时，电流表读数为I．已知流体的电阻率为ρ，不计电流表的内阻，则流体的流量Q可表示为（ ）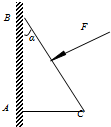
如图所示，横截面为直角三角形的物块ABC，AB边靠在竖直墙面上，F是垂直于斜面BC的推力，这时物块静止不动．假设物块受到的最大静摩擦力与滑动摩擦力相等，现将力F增大，以下说法正确的是（ ）
如图所示，横截面为四分之一圆（半径为R）的柱体放在水平地面上，一根匀质木棒OA长为3R，重为G．木棒的O端与地面上的铰链连接，木棒搁在柱体上，各处摩擦均不计．现用一水平推力F作用在柱体竖直面上，使柱体沿着水平地面向左缓慢移动．问：