题目内容
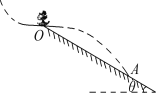
【题目】如图所示，竖直平面内有一段不光滑的斜直轨道与光滑的圆形轨道相切，切点P与圆心O的连线与竖直方向的夹角为θ＝60°，圆形轨道的半径为R，一质量为m的小物块从斜轨道上A点由静止开始下滑，然后沿圆形轨道运动，A点相对圆形轨道底部的高度h＝7R，物块通过圆形轨道最高点C时，与轨道间的压力大小为3mg.求：
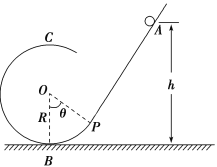
(1)物块通过轨道最高点时的速度大小？
(2)物块通过轨道最低点B时对轨道的压力大小？
(3)物块与斜直轨道间的动摩擦因数μ＝？
【答案】(1)
(2)
(3)
【解析】
（1）对物块通过轨道最高点C时受力C点：N+mg＝
得：νc＝2
（2）从最低点B到最高点C：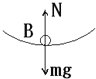
2mgR＝
物块通过轨道最低点B时：NBmg＝
得：NB=9mg
根据牛顿第三定律，物块通过轨道最低点B时对轨道的压力大小为9mg
（3）根椐动能定理，由A运动到B有：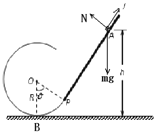
mghμmgcosθS＝
0
Ssinθ=h-R+Rcosθ
解得μ=
练习册系列答案
天天练口算系列答案
相关题目
