题目内容
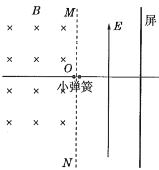
【题目】如图所示，在竖直分界线
的左侧有垂直纸面的匀强磁场，竖直屏与之间有方向向上的匀强电场。在
处有两个带正电的小球
和
，两小球间不发生电荷转移。若在两小球间放置一个被压缩且锁定的小型弹簧（不计弹簧长度），解锁弹簧后，两小球均获得沿水平方向的速度。已知小球的质量是小球的
倍，电荷量是小球的
倍。若测得小球在磁场中运动的半径为
，小球击中屏的位置的竖直偏转位移也等于。两小球重力均不计。
(1)将两球位置互换，解锁弹簧后，小球在磁场中运动，求两球在磁场中运动半径之比、时间之比；
(2)若小球向左运动求、两小球打在屏上的位置之间的距离。
【答案】(1)
，
；(2)
【解析】
(1)两小球静止反向弹开过程，系统动量守恒有
①
小球A、B在磁场中做圆周运动，分别有
，
②
解①②式得
磁场运动周期分别为
，
解得运动时间之比为
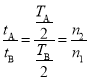
(2)如图所示，小球A经圆周运动后，在电场中做类平抛运动。
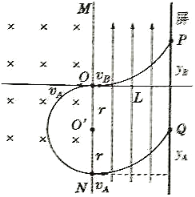
水平方向有
③
竖直方向有
④
由牛顿第二定律得
⑤
解③④⑤式得
⑥
小球B在电场中做类平抛运动，同理有
⑦
由题意知
⑧
应用几何关系得
⑨
解①⑥⑦⑧⑨式得
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
