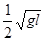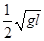题目内容
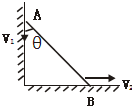 如图所示,一个长直轻杆AB在墙角沿竖直墙和水平地面滑动,当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为V1,B端沿地面的速度大小为V2,则V1、V2的关系是
如图所示,一个长直轻杆AB在墙角沿竖直墙和水平地面滑动,当AB杆和墙的夹角为θ时,杆的A端沿墙下滑的速度大小为V1,B端沿地面的速度大小为V2,则V1、V2的关系是V1=V2tanθ
V1=V2tanθ
.分析:将A、B两点的速度分解为沿杆子方向和垂直于杆子方向,抓住两点沿杆子方向上的分速度相等,求出v1和v2的关系.
解答:解:将A点的速度分解为沿杆子方向和垂直于杆子方向,在沿杆子方向上的分速度为v1∥=v1cosθ,将B点的速度分解为沿杆子方向和垂直于杆子方向,在沿杆子方向上的分速度v2∥=v2sinθ.由于v1∥=v2∥,所以v1=v2tanθ.
故答案为:v1=v2tanθ.
故答案为:v1=v2tanθ.
点评:解决本题的关键将A、B两点的速度分解为沿杆子方向和垂直于杆子方向,以及知道沿杆子方向上的两个分速度大小相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
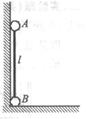
如图所示,一个长直轻杆两端分别固定一个小球A和B,两球质量均为m,两球半径忽略不计,杆的长度为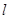 。先将杆AB竖直靠放在竖直墙上,轻轻振动小球B,使小球B在水平面上由静止开始向右滑动,当小球A沿墙下滑距离为
。先将杆AB竖直靠放在竖直墙上,轻轻振动小球B,使小球B在水平面上由静止开始向右滑动,当小球A沿墙下滑距离为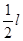 时,下列说法正确的是( )
时,下列说法正确的是( )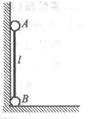
A.小球A和B的速度都为 |
B.小球A和B的速度都为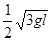 |
C.小球A的速度为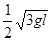 ,小球B的速度为 ,小球B的速度为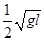 |
D.小球A的速度为 ,小球B的速度为 ,小球B的速度为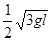 |
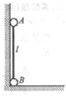 如图所示,一个长直轻杆两端分别固定一个小球A和B,两球质量均为m,两球半径忽略不计,杆的长度为l.先将杆AB竖直靠放在竖直墙上,轻轻振动小球B,使小球B在水平面上由静止开始向右滑动,当小球A沿墙下滑距离为
如图所示,一个长直轻杆两端分别固定一个小球A和B,两球质量均为m,两球半径忽略不计,杆的长度为l.先将杆AB竖直靠放在竖直墙上,轻轻振动小球B,使小球B在水平面上由静止开始向右滑动,当小球A沿墙下滑距离为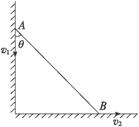
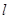 。先将杆AB竖直靠放在竖直墙上,轻轻振动小球B,使小球B在水平面上由静止开始向右滑动,当小球A沿墙下滑距离为
。先将杆AB竖直靠放在竖直墙上,轻轻振动小球B,使小球B在水平面上由静止开始向右滑动,当小球A沿墙下滑距离为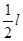 时,下列说法正确的是(
)
时,下列说法正确的是(
)