题目内容
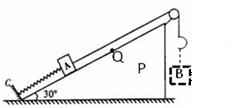
如图所示,P是倾角为30°的光滑固定斜面.劲度系数为k的轻弹簧一端固定在斜面底端的固定挡板C上,另一端与质量为m的物块A相连接.细绳的一端系在物体A上,细绳跨过不计质量和摩擦的定滑轮,另一端有一个不计质量的小挂钩.小挂钩不挂任何物体时,物体A处于静止状态,细绳与斜面平行.在小挂钩上轻轻挂上一个质量也为m的物块B后,物块A沿斜面向上运动.斜面足够长,运动过程中B始终未接触地面.已知重力加速度为g,问:
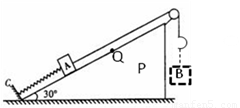
(1)求物块A刚开始运动时的加速度大小a.
(2)设物块A沿斜面上升通过Q点位置时速度最大,求Q点到出发点的距离x0及最大速度vm.
(3)把物块B的质量变为原来的N倍(N>0.5),小明同学认为,只要N足够大,就可以使物块A沿斜面上滑到Q点时的速度增大到2vm,你认为是否正确?如果正确,请说明理由,如果不正确,请求出A沿斜面上升到Q点位置的速度的范围.
(1)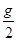 (2)
(2)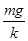 ;
;
(3)不正确.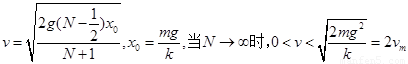
【解析】
试题分析:(1)设绳的拉力大小为T,分别以A、B为对象用牛顿第二定律,T=ma,mg-T=ma(2)A加速上升阶段,弹簧恢复原长前对A用牛顿第二定律T+kx-mg/2=ma,对B用牛顿第二定律mg-T=ma,消去T得mg/2+kx=2ma,上升过程x减小,a减小,v增大;弹簧变为伸长后同理得mg/2-kx=2ma,上升过程x增大,a减小,v继续增大,当kx=mg/2时a=0,速度达到最大。可见Q点时速度最大,对应的弹力大小恰好是mg/2,弹性势能和初始状态相同。A上升到Q点过程,A、B的位移大小都是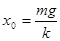 ,该过程对A、B和弹簧系统用机械能守恒定律,
,该过程对A、B和弹簧系统用机械能守恒定律,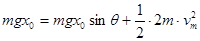 ,可得vm⑶A上升到Q点过程,仍对该过程用机械能守恒,
,可得vm⑶A上升到Q点过程,仍对该过程用机械能守恒,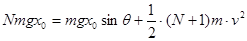 ,解得
,解得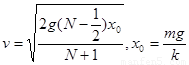 ,当
,当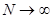 时,有
时,有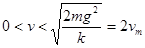
考点:计算题
点评:本题难度中等,处理连接体问题时,抓住整体加速度大小与各部分加速度大小相等,利用牛顿第二定律列公式求解是关键,利用机械能守恒定律求解问题时,要注意初末位置的能量变化

 名校课堂系列答案
名校课堂系列答案 如图所示,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可视为质点)从直轨道的P点由静止释放,结果它在两轨道之间做往复运动.已知P点与圆弧的圆心O等高,物体与轨道AB间的动摩擦因素为μ,求:
如图所示,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可视为质点)从直轨道的P点由静止释放,结果它在两轨道之间做往复运动.已知P点与圆弧的圆心O等高,物体与轨道AB间的动摩擦因素为μ,求: