题目内容
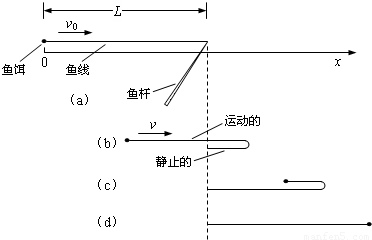
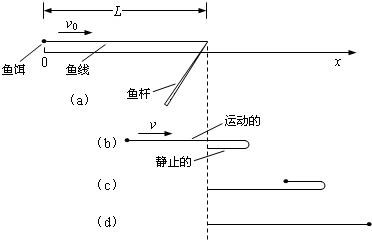
钓鱼时甩杆后鱼饵飞出的过程可想象成这样的情景,开始时鱼线水平向左伸展并以初始速率v0向右运动(如图a所示),当鱼线端的鱼饵水平向前运动时,鱼线会弯折成水平的上下两段(如图b所示),上段鱼线随鱼饵仍向前运动,而下段鱼线则静止,下段鱼线的长度增加时上段鱼线的长度减小(如图c所示),直到鱼线水平向右完全伸开(如图d所示).若不考虑空气阻力等其它因素,则在上述过程中图a中鱼线的动能将逐渐集中于鱼饵和长度不断减小的上段鱼线,已知初始速率v0=6.0m/s,鱼线长L=20m,鱼饵的质量m=0.8g,假定鱼线的质量分布均匀,其线密度(单位长度的质量)ρ=1.3g/m.关于上述鱼饵飞出的过程,
(1)求出鱼饵能达到的最大速率.
(2)采用已给出的x轴(原点在图a中的鱼饵处),写出鱼饵的速率随x变化的函数式,并说明x的取值范围.
(1)求出鱼饵能达到的最大速率.
(2)采用已给出的x轴(原点在图a中的鱼饵处),写出鱼饵的速率随x变化的函数式,并说明x的取值范围.

分析:(1)当鱼饵达到的最大速率时,绳子处于静止状态,初始位置时绳子和鱼饵的动能全部转化为末位置鱼饵的动能,根据能量守恒列式即可求解.
(2)在运动过程中总动能是守恒的,任一个位置的动能都等于初始位置的总动能,根据能量守恒列式即可求解.
(2)在运动过程中总动能是守恒的,任一个位置的动能都等于初始位置的总动能,根据能量守恒列式即可求解.
解答:解:(1)当鱼饵达到的最大速率时,绳子处于静止状态,根据能量守恒列式得:
m
+
ρL
=
m
,
带入数据得:
×0.8×10-3×6.02+
×1.3×10-3×20×6.02=
×0.8×10-3×
解得:vM≈34.7m/s
(2)在运动过程中总动能是守恒的,则有:
m
+
ρL
=
mv2+
ρ(L-
)v2
带入数据得:
解得:v=
,0≤x≤40m
答:(1)鱼饵能达到的最大速率为34.7m/s.
(2)鱼饵的速率随x变化的函数式为,v=
,0≤x≤40m.
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 M |
带入数据得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 M |
解得:vM≈34.7m/s
(2)在运动过程中总动能是守恒的,则有:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
带入数据得:
|
解得:v=
|
答:(1)鱼饵能达到的最大速率为34.7m/s.
(2)鱼饵的速率随x变化的函数式为,v=
|
点评:本题是信息题,要求同学们能读懂题目的意思,其中下段鱼线静止是解题的突破口,难度适中.

练习册系列答案
相关题目