Question

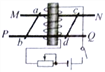
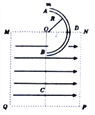
【题目】如图所示，矩形区域MNPQ内有水平向右的匀强电场，虚线框外为真空区域。半径为R，内壁光滑、内径很小的绝缘半圆管ADB固定在整直平面内，直径AB垂直于水平虚线MN，圆心0恰在MN的中点，半圆管的一半处于电场中，一质量为m，可视为质点的带正电，电荷量为q的小球从半圆管的A点由静止开始滑入管内，小球从B点穿出后，能够通过B点正下方的C点。重力加速度为g，小球在C点处的加速度大小为.则下列说法正确的是

A. 匀强电场的场强E为

B. 小球在到达B点时，半圆轨道对它作用力的大小

C. 球流够到达B点正下方C点，虚线标MNPQ的高度不大于

D. 从B点开始计时，小球从B运动到C点的过程中，经过时间时动能最小

Answer 1

【答案】BD

【解析】由于小球在C处受到重力和电场力的共同作用，所以C点：

F合＝ma＝
代入数据得：E＝，选项A错误；
A→B的过程重力和电场力对小球做功，mg(2R)FR＝mvB2
得：vB＝
在B点Nmg＝
半圆轨道对小球的作用力 N＝mg，选项B正确；

小球从B→C水平方向匀减速运动，竖直方向自由落体运动，ax＝g；ay=g
设向左减速时间为

y＝g(2t)2＝

宽度应满足条件L＞2R，高度满足条件H≥R，选项C错误；

当F与mg的合力与v垂直时，小球的动能最小，设经过的时间为t，则vy＝vx ； vy=gt

vx＝vBgt ∴t＝ ，选项D正确；故选BD.