题目内容
北京正负电子对撞机是目前国际上唯一高亮度正负电子对撞机,因此作为世界上一个重要的高能物理实验研究基地对国外开放.正、负电子对撞机由直线加速器P、电子分离器Q、环形储存器M和对撞室D组成,如图所示,P、加速器出口O、环心O′、D在一条直线上.被加速器P加速后的正、负电子相隔时间t0先后由O点以相同速度v0进入电子分离器Q,分离后分别沿圆环切线方向由a、b注入M,在M中恰沿环做圆周运动运动,最终在D中实现对撞.为了实现正、负电子的分离和在环形储存器内的圆周运动,并保证正、负电子在D中相遇,在环外分离器Q区域和环内区域分别加有匀强磁场B1和B2.已知图中∠O1O′O=∠O2O′O=30°,电子质量为m,电荷量为e,环的半径R远大于环管半径r,除在D中碰撞外忽略电子间的相互作用,求: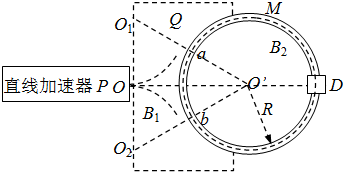
(1)Q、M区域内的磁感应强度B1、B2及B1与B2的方向关系;
(2)环的最大半径R.

(1)Q、M区域内的磁感应强度B1、B2及B1与B2的方向关系;
(2)环的最大半径R.
分析:(1)由几何关系找到在Q和M区域中圆周运动的半径大小关系,进而得到R1=R,结合正、负电子从O第一次到D的时间关系解得两磁场磁感应强度的大小,由电子偏转方向可判断,Q、M中磁感应强度的方向相反.
(2)根据问题(1)中的关系,表示出R的关系式,进而得到R的最大值.
(2)根据问题(1)中的关系,表示出R的关系式,进而得到R的最大值.
解答:解:(1)设电子在分离器中偏转的轨道半径为R1,在rt△OO'O1中,R1=O1O=
O1O′=
(R1+R)①
所以R1=R故B=
=B1=B2②
因此电子在Q和M中运动的周期相同,且T=
③
正、负电子从O第一次到D的时间为△t=
+
=
相等,因此要让正、负电子在D中相遇,有 t1-t2=t0=nT(n=1,2,3…)
由②③④解得B1=B2=
④(n=1,2,3…)
由电子偏转方向可判断,Q、M中磁感应强度的方向相反
(2)由②④得 R=
=
(n=1,2,3…)
n=1时,环的半径最大,且 Rm=
答:(1)B1=B2=
④(n=1,2,3…),Q、M中磁感应强度的方向相反;
(2)半径最大为 Rm=
.
| 1 |
| 2 |
| 1 |
| 2 |
所以R1=R故B=
| mv0 |
| qR |
因此电子在Q和M中运动的周期相同,且T=
| 2πm |
| eB1 |
正、负电子从O第一次到D的时间为△t=
| T |
| 6 |
| 5T |
| 12 |
| 7T |
| 12 |
由②③④解得B1=B2=
| 2nπm |
| et0 |
由电子偏转方向可判断,Q、M中磁感应强度的方向相反
(2)由②④得 R=
| mv |
| eB1 |
| v0t0 |
| 2nπ |
n=1时,环的半径最大,且 Rm=
| v0t0 |
| 2π |
答:(1)B1=B2=
| 2nπm |
| et0 |
(2)半径最大为 Rm=
| v0t0 |
| 2π |
点评:主要考查了带电粒子在匀强磁场中运动的问题,要求同学们能正确分析粒子的运动情况,会应用几何知识找到半径,熟练掌握圆周运动基本公式.

练习册系列答案
相关题目
北京正负电子对撞机的核心部分是使电子加速的环形室,若一电子在环形室中作半径为R的圆周运动,转了1圈回到原位置,则其位移和路程分别是( )
| A、0,2πR | B、2πR,2πR | C、2R,2R | D、2R,2πR |

