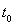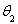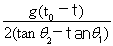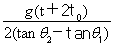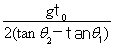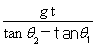题目内容
水平抛出的小球,t秒末的速度方向与水平方向的夹角为θ1,t+t0秒末速度方向与水平方向的夹角为θ2,忽略空气阻力,则小球初速度的大小为( )
| A、gt0(cosθ1-cosθ2) | ||
B、
| ||
| C、gt0(tanθ1-tanθ2) | ||
D、
|
分析:设水平方向上的速度为v0,根据平行四边形定则求出t秒末、(t+△t)秒末竖直方向上的分速度,根据△vy=g△t求出小球的初速度.
解答:解:设水平方向上的速度为v0,t秒末速度方向与水平方向的夹角为θ1,
则竖直方向上的分速度:vy1=v0tanθ1,
(t+△t)秒末速度方向与水平方向的夹角为θ2,
则竖直方向上的分速度:vy2=v0tanθ2.
根据vy2-vy1=g△t得:v0=
.
故D正确,A、C、D错误.
故选:B.
则竖直方向上的分速度:vy1=v0tanθ1,
(t+△t)秒末速度方向与水平方向的夹角为θ2,
则竖直方向上的分速度:vy2=v0tanθ2.
根据vy2-vy1=g△t得:v0=
| g△t |
| tanθ2-tanθ1 |
故D正确,A、C、D错误.
故选:B.
点评:解决本题的关键掌握平抛运动的规律,知道平抛运动在竖直方向上做自由落体运动,在水平方向上做匀速直线运动.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
水平抛出的小球,t秒末的速度方向与水平方向的夹角为θ1,t+t0秒末速度方向与水平方向的夹角为θ2,忽略空气阻力,则小球初速度的大小为( )
| A.gt0(cosθ1-cosθ2) | B. |
| C.gt0(tanθ1-tanθ2) | D.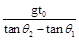 |