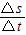题目内容
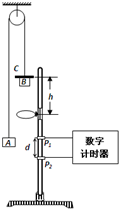 用如图装置可验证机械能守恒定律.轻绳两端系着质量相等的物块A、B,物块B上放置一金属片C.铁架台上固定一金属圆环,圆环处在物块B正下方.系统静止时,金属片C与圆环间的高度差为h.由此释放,系统开始运动,当物块B穿过圆环时,金属片C被搁置在圆环上.两光电门固定在铁架台P1、P2处,通过数字计时器可测出物块B通过P1、P2这段时间.
用如图装置可验证机械能守恒定律.轻绳两端系着质量相等的物块A、B,物块B上放置一金属片C.铁架台上固定一金属圆环,圆环处在物块B正下方.系统静止时,金属片C与圆环间的高度差为h.由此释放,系统开始运动,当物块B穿过圆环时,金属片C被搁置在圆环上.两光电门固定在铁架台P1、P2处,通过数字计时器可测出物块B通过P1、P2这段时间.(1)若测得P1、P2之间的距离为d,物块B通过这段距离的时间为t,则物块B刚穿过圆环后的速度v=
(2)若物块A、B的质量均为M表示,金属片C的质量用m表示,该实验中验证了下面哪个等式成立,即可验证机械能守恒定律.正确选项为
A.mgh=
| 1 |
| 2 |
C.mgh=
| 1 |
| 2 |
| 1 |
| 2 |
(3)本实验中的测量仪器除了刻度尺、光电门、数字计时器外,还需要
(4)改变物块B的初始位置,使物块B由不同的高度落下穿过圆环,记录各次高度差h以及物块B通过P1、P2这段距离的时间为t,以h为纵轴,以
分析:(1)通过平均速度等于瞬时速度,即可求解;
(2)根据系统减小的重力势能,转化为系统增加的动能,即可求解;
(3)根据上式可知,还需要天平测出金属片C的质量;
(4)根据下降的高度求出重力势能的减小量,根据某段时间内平均速度等于中间时刻的瞬时速度求出C点的瞬时速度,从而求出动能的增加量,进而列出表达式,由此可确定横轴及图象的斜率.
(2)根据系统减小的重力势能,转化为系统增加的动能,即可求解;
(3)根据上式可知,还需要天平测出金属片C的质量;
(4)根据下降的高度求出重力势能的减小量,根据某段时间内平均速度等于中间时刻的瞬时速度求出C点的瞬时速度,从而求出动能的增加量,进而列出表达式,由此可确定横轴及图象的斜率.
解答:解:(1)根据平均速度等于瞬时速度,则有:物块B刚穿过圆环后的速度v=
;
(2)由题意可知,系统ABC减小的重力势能转化为系统的增加的动能,即为:mgh+Mgh-Mgh=
(2M+m)v2,即为:mgh=
(2M+m)v2,故C正确;
(3)由mgh=
(2M+m)v2,公式可知,除了刻度尺、光电门、数字计时器外,还需要天平测出金属片的质量;
(4)将mgh=
(2M+m)v2,变形后,则有:h=
?
;因此以
为横轴;
由上式可知,作出的图线是一条过原点的直线,直线的斜率k=(2M+m)
.
故答案为:(1)
(2)C (3)天平(4)
;(2M+m)
.
| d |
| t |
(2)由题意可知,系统ABC减小的重力势能转化为系统的增加的动能,即为:mgh+Mgh-Mgh=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由mgh=
| 1 |
| 2 |
(4)将mgh=
| 1 |
| 2 |
| (2M+m)d2 |
| 2mg |
| 1 |
| t2 |
| 1 |
| t2 |
由上式可知,作出的图线是一条过原点的直线,直线的斜率k=(2M+m)
| d2 |
| 2 mg |
故答案为:(1)
| d |
| t |
| 1 |
| t2 |
| d2 |
| 2 mg |
点评:考查平均速度等于瞬时速度,条件是时间很短或做匀变速直线运动;掌握系统机械能守恒定律验证方法,注意由于A与B的质量相同,则重力势能之和不变;并学会运用数学表达式来分析,理解图象的斜率的含义.

练习册系列答案
相关题目

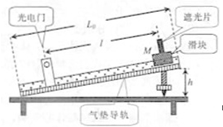 气垫导轨可以在导轨和滑块之间形成一薄层空气膜,使滑块和导轨间的摩擦几乎为零,如图所示,让滑块从气垫导轨的某一高度下滑,滑块上的遮光片的宽度为△s,当遮光片通过电门时与光电门相连的数字毫秒器显示遮光时间为△t,则遮光片通过光电门的平均速度为v=
气垫导轨可以在导轨和滑块之间形成一薄层空气膜,使滑块和导轨间的摩擦几乎为零,如图所示,让滑块从气垫导轨的某一高度下滑,滑块上的遮光片的宽度为△s,当遮光片通过电门时与光电门相连的数字毫秒器显示遮光时间为△t,则遮光片通过光电门的平均速度为v=