Question

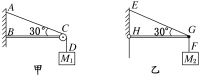
【题目】如图所示，将质量为m的小球用轻绳挂在倾角为α＝30°的光滑斜面上，则：

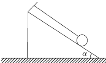
(1)当斜面以加速度a＝2g水平向左运动时,求:小球对斜面的压力大小及绳中的拉力大小。

(2)当斜面以加速度a＝0.5g水平向右运动时,求:小球对斜面的压力大小及绳中的拉力大小。

Answer 1

【答案】（1）FN1=0；FT1=mg （2）

【解析】

只要有水平向右的力作用在斜面上小球就会随斜面一起做匀加速运动，要是小球在斜面，则当斜面对小球的支持力为零时，加速度最大，对小球进行受力分析求出最大加速度，再根据牛顿第二定律以及力的分解求解各个情况下小球对斜面的压力及绳中的拉力大小；

（1）当小球对斜面的压力为零时，小球只受重力和拉力，合力水平向,

解得；

所以当向左的加速度a≥时，斜面对小球无弹力，而a=2g>，则小球要飘起来，即；

小球只受重力和绳的拉力，合力水平向右，据几何关系可知，绳拉力F、重力和二力的合力构成直角三角形，得：，

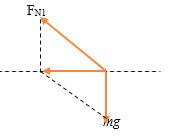
（2）斜面水平向右运动时，当绳中张力恰好为零时可得临界加速度为；而，则小球受拉力及支持力，

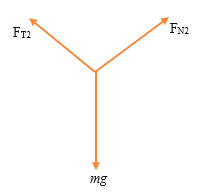
根据牛顿第二定律可得①；②

联立解得，根据牛顿第三定律可得小球对斜面的压力大小为