题目内容
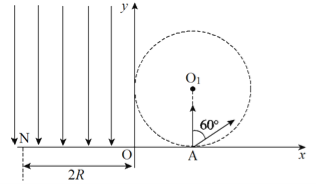
【题目】空间中有一直角坐标系，其第一象限中在圆心为O1、半径为R、边界与x轴和y轴相切的圆形区域内有垂直于纸面向里的匀强磁场（图中未画出），磁感应强度大小为B，第二象限中存在方向竖直向下的匀强电场。现有一群质量为m、电荷量为q的带正电的粒子从圆形区域边界与x轴的切点A处沿纸面上的不同方向射入磁场中，如图所示。已知粒子在磁场中做匀速圆周运动的半径均为R，其中沿AO1方向射入的粒子恰好到达x轴上与O点距离为2R的N点。不计粒子的重力和它们之间的相互作用。求：
（1）粒子射入磁场时的速度大小及电场强度的大小；
（2）速度方向与AO1夹角为60°（斜向右上方）的粒子到达x轴所用的时间。
【答案】（1）
、
（2）
【解析】
试题分析：(1）设粒子射入磁场时的速度大小为v，因在磁场中做匀速圆周运动的半径为R，由牛顿第二定律得
，得
如图甲所示，因粒子的轨迹半径是R，故沿AO1方向射入的粒子一定从与圆心等高的D点沿x轴负方向射入电场，则粒子在电场中从D点到N点做类平抛运动，有
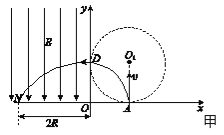
又因为
解得
（2分）
(2）轨迹如图所示
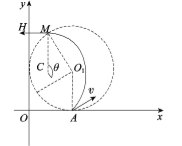
对于速度v(斜向右上方）的粒子，轨迹如图乙所示，轨迹圆心为C，从M点射出磁场，连接O1M，四边形O1MCA是菱形，故CM垂直于x轴，速度方向偏转角度等于圆心角θ＝150°，
速度为v的粒子在磁场中运动的时间为
粒子离开磁场到y轴的距离MH＝
，在无场区运动的时间
设粒子在电场中到达x轴运动的时间为t3，
，
，
故粒子到达x轴的时间为
t＝t1＋t2＋t3＝
练习册系列答案
津桥教育计算小状元系列答案
相关题目
