题目内容
3. 在竖直墙壁间有半圆球A和圆球B,其中圆球B的表面光滑,半圆球A与左侧墙壁之间的动摩擦因数为$\frac{2}{5}$$\sqrt{3}$.两球心之间连线与水平方向成30°的夹角,两球恰好不下滑,设最大静摩擦力等于滑动摩擦力,则半球圆A和圆球B的质量之比为( )
在竖直墙壁间有半圆球A和圆球B,其中圆球B的表面光滑,半圆球A与左侧墙壁之间的动摩擦因数为$\frac{2}{5}$$\sqrt{3}$.两球心之间连线与水平方向成30°的夹角,两球恰好不下滑,设最大静摩擦力等于滑动摩擦力,则半球圆A和圆球B的质量之比为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
分析 隔离光滑均匀圆球B,对B受力分析,根据平衡条件列式求解FN,对两球组成的整体进行受力分析,根据平衡条件列式求解即可.
解答 解:设A的质量为m,B的质量为M,
隔离光滑均匀圆球B,对B受力分析如图所示,可得:
FN=Fcosθ
Mg-Fsinθ=0
解得:FN=$\frac{Mg}{tanθ}$,
对两球组成的整体有:
(m+M)g-μFN=0
代入数据,联立解得:$\frac{m}{M}=\frac{1}{5}$
故选:C.
点评 解决本题的关键能够正确地受力分析,运用共点力平衡进行求解,掌握整体法和隔离法的运用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
13.在限速20km/h的地段,警察拦住一超速车对司机说:“先生,你刚才的车速是30km/h,已超速…”司机辩解说:“这段路很堵,我半小时才走5km,怎么会超速?…”以下观点不正确的是( )
| A. | 限速20km/h,表示该路段上行驶时,车辆允许的最大瞬时速度是20km/h | |
| B. | 从司机的辩解可以看出,司机可能没有弄清楚瞬时速度与平均速度的区别 | |
| C. | 物体在某位置的瞬时速度就是物体在该位置附近极短时间内的平均速度的极限 | |
| D. | 如果该司机真的由于堵车在半小时内才走5km,他不可能超速 |
18.如图所示,某带电粒子p恰能静止于电容器两极板之间,欲使该粒子向上运动,采取的措施可能是( )


| A. | 只需向左滑动滑动变阻器触头即可 | |
| B. | 只需将电容器两极板靠近些即可 | |
| C. | 断开开关,再将两极板靠近一些 | |
| D. | 断开开关,将上极板向右拉一段距离 |
15. 如图所示,电源电动势E=12V,内阻r=3Ω,甲图中R0=1Ω,乙图中额定输出功率P0=2W的直流电动机绕阻R0′=1Ω.当调节滑动变阻器R1时,可使甲电路输出功率最大;调节R2时可使乙电路输出功率最大,且此时电动机刚好正常工作.则( )
如图所示,电源电动势E=12V,内阻r=3Ω,甲图中R0=1Ω,乙图中额定输出功率P0=2W的直流电动机绕阻R0′=1Ω.当调节滑动变阻器R1时,可使甲电路输出功率最大;调节R2时可使乙电路输出功率最大,且此时电动机刚好正常工作.则( )
 如图所示,电源电动势E=12V,内阻r=3Ω,甲图中R0=1Ω,乙图中额定输出功率P0=2W的直流电动机绕阻R0′=1Ω.当调节滑动变阻器R1时,可使甲电路输出功率最大;调节R2时可使乙电路输出功率最大,且此时电动机刚好正常工作.则( )
如图所示,电源电动势E=12V,内阻r=3Ω,甲图中R0=1Ω,乙图中额定输出功率P0=2W的直流电动机绕阻R0′=1Ω.当调节滑动变阻器R1时,可使甲电路输出功率最大;调节R2时可使乙电路输出功率最大,且此时电动机刚好正常工作.则( )| A. | R1=2Ω | B. | R1=1.5Ω | C. | R2=1.5Ω | D. | R2=2Ω |
9.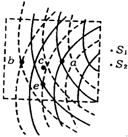 两列简谐横波,波源的振动频率相同,如图为某时刻两列波在介质中相遇的情景,实线表示波峰,虚线表示波谷,则下面说法正确的是( )
两列简谐横波,波源的振动频率相同,如图为某时刻两列波在介质中相遇的情景,实线表示波峰,虚线表示波谷,则下面说法正确的是( )
 两列简谐横波,波源的振动频率相同,如图为某时刻两列波在介质中相遇的情景,实线表示波峰,虚线表示波谷,则下面说法正确的是( )
两列简谐横波,波源的振动频率相同,如图为某时刻两列波在介质中相遇的情景,实线表示波峰,虚线表示波谷,则下面说法正确的是( )| A. | a、b点是干涉加强的位置,c点振动最弱 | |
| B. | 当振源的振动频率同时增加时,干涉区域的干涉图样不发生任何变化 | |
| C. | 再过$\frac{T}{4}$,a、b将变成振动减弱的位置,e点的振动将加强 | |
| D. | a、b、c点是干涉加强的位置,e点振动最弱 |
10.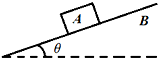 如图所示,木块A静止在倾斜的木板B上,现将B的倾角θ缓慢增大10°,A仍静止在木板上,与原来相比,下列说法中正确的是( )
如图所示,木块A静止在倾斜的木板B上,现将B的倾角θ缓慢增大10°,A仍静止在木板上,与原来相比,下列说法中正确的是( )
 如图所示,木块A静止在倾斜的木板B上,现将B的倾角θ缓慢增大10°,A仍静止在木板上,与原来相比,下列说法中正确的是( )
如图所示,木块A静止在倾斜的木板B上,现将B的倾角θ缓慢增大10°,A仍静止在木板上,与原来相比,下列说法中正确的是( )| A. | A受到的静摩擦力变小,B对A的支持力也变小 | |
| B. | A受到的静摩擦力变大,B对A的支持力也变大 | |
| C. | A受到的静摩擦力变小,B对A的支持力变大 | |
| D. | A受到的静摩擦力变大,B对A的支持力变小 |
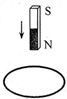 如图所示,桌面上放一100匝线圈,线圈中心上方一定高度处有一竖立的条形磁体.当磁体竖直向下运动时,穿过线圈的磁通量将变大还是变小?.在上述过程中,穿过线圈的磁通量变化了0.1Wb,经历的时间为0.5s,则线圈中的感应电动势为多少伏?
如图所示,桌面上放一100匝线圈,线圈中心上方一定高度处有一竖立的条形磁体.当磁体竖直向下运动时,穿过线圈的磁通量将变大还是变小?.在上述过程中,穿过线圈的磁通量变化了0.1Wb,经历的时间为0.5s,则线圈中的感应电动势为多少伏?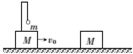 如图所示,光滑水平地面上,在质量M=1kg的滑块上用轻杆及轻绳悬吊质量m=0.5kg的小球.此装置以速度v0=2m/s向右滑动.另一质量也为M的滑块静止于上述装置的右侧.当两滑块相撞后,便粘在一起向右运动,求
如图所示,光滑水平地面上,在质量M=1kg的滑块上用轻杆及轻绳悬吊质量m=0.5kg的小球.此装置以速度v0=2m/s向右滑动.另一质量也为M的滑块静止于上述装置的右侧.当两滑块相撞后,便粘在一起向右运动,求