题目内容
 (2010?南昌一模)如图所示,A、B为两块水平放置的平行金属板,A板带正电、B板带负电.两板之间存在着匀强屯场,两板间距为d、电势差为U、在B板上开有两个间距为L的小孔.在B板外侧两孔的中点上固定某一点电荷Q.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电微粒(微粒的重力不计,点电荷电场不受金属板的影响),问:
(2010?南昌一模)如图所示,A、B为两块水平放置的平行金属板,A板带正电、B板带负电.两板之间存在着匀强屯场,两板间距为d、电势差为U、在B板上开有两个间距为L的小孔.在B板外侧两孔的中点上固定某一点电荷Q.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电量为q的带正电微粒(微粒的重力不计,点电荷电场不受金属板的影响),问:(1)微粒穿过B极小孔时的速度多大;
(2)若微粒恰能从另一小孔进入.求点电荷Q的电性和电量.
(3)从释放微粒开始,经过多长时间微粒会通过轨迹的最低点,试写出时间满足的条件.
分析:(1)运用动能定理研究微粒在加速电场的过程;
(2)微粒穿出B孔,受到点电荷的引力,库仑力提供向心力,列出等式即可求解;
(3)匀加速直线运动和匀速圆周运动运用各自的规律求解时间.
(2)微粒穿出B孔,受到点电荷的引力,库仑力提供向心力,列出等式即可求解;
(3)匀加速直线运动和匀速圆周运动运用各自的规律求解时间.
解答:解:(1)设微粒穿过B板小孔时的速度为v,根据动能定理,有:
qU=
mv2
解得:v=
(2)微粒穿出B孔,点电荷Q对q是引力,所以Q的电性与q相反,应带负电;
微粒穿出B孔,在B板下做圆周运动,库仑力提供向心力;由于Q在B板外侧两孔的中点上,Q与q之间的距离为
所以得:
=m
代人数据,整理得:Q=
(3)微粒从释放开始经t1射出B板的小孔,则:t1=
=
=2d
设微粒在B板下做匀速圆周运动经过t2到达最低点P点,
则:t2=
=
=
所以从释放微粒开始,经过t=t1+t2=(2d+
)
微粒到达P点.
答:(1)微粒穿过B板小孔时的速度为v=
;
(2)Q带负电荷,电量为:Q=
;
(3)从释放微粒开始,经过t=t1+t2=(2d+
)
微粒到达P点.
qU=
| 1 |
| 2 |
解得:v=
|
(2)微粒穿出B孔,点电荷Q对q是引力,所以Q的电性与q相反,应带负电;
微粒穿出B孔,在B板下做圆周运动,库仑力提供向心力;由于Q在B板外侧两孔的中点上,Q与q之间的距离为
| L |
| 2 |
所以得:
| kQq | ||
(
|
| v2 | ||
(
|
代人数据,整理得:Q=
| 2U |
| k |
(3)微粒从释放开始经t1射出B板的小孔,则:t1=
| d | ||
|
| d | ||
|
|
设微粒在B板下做匀速圆周运动经过t2到达最低点P点,
则:t2=
| ||||
| v |
| πL |
| 4v |
| πL |
| 4 |
|
所以从释放微粒开始,经过t=t1+t2=(2d+
| πL |
| 4 |
|
答:(1)微粒穿过B板小孔时的速度为v=
|
(2)Q带负电荷,电量为:Q=
| 2U |
| k |
(3)从释放微粒开始,经过t=t1+t2=(2d+
| πL |
| 4 |
|
点评:了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.
圆周运动问题的解决析关键要通过受力分析找出向心力的来源.
圆周运动问题的解决析关键要通过受力分析找出向心力的来源.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 (2010?南昌一模)如图所示,一长为L、质量为m的柔软匀质物体从光滑的水平面上以初速度v0向右滑上同一水平的台面,物体前端在台面上滑动S距离停下来.物体与台面间的动摩擦因数为μ而且S>L,则物体的初速度v0为( )
(2010?南昌一模)如图所示,一长为L、质量为m的柔软匀质物体从光滑的水平面上以初速度v0向右滑上同一水平的台面,物体前端在台面上滑动S距离停下来.物体与台面间的动摩擦因数为μ而且S>L,则物体的初速度v0为( )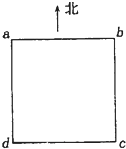 (2010?南昌一模)在北半球某处上方的地磁场,磁感应强度大小为B,方向与竖直方向的夹角为θ.一边长为L的正方形线框水平放置.如图所示(所示纸面为水平面).现在使线框在t时间内,以cd边为固定转轴,ab边绕轴向上转过90°角,则在这一过程中,线框中产生的平均电动势为
(2010?南昌一模)在北半球某处上方的地磁场,磁感应强度大小为B,方向与竖直方向的夹角为θ.一边长为L的正方形线框水平放置.如图所示(所示纸面为水平面).现在使线框在t时间内,以cd边为固定转轴,ab边绕轴向上转过90°角,则在这一过程中,线框中产生的平均电动势为 (2010?南昌一模)如图所示,A,B两木块质量分别为4kg和1kg,C板的质量为5kg,A、C之间的动摩擦因数为0.25,桌面光滑,A、C静止时,将木块B由张紧状态抬高0.8m后释放,滑轮的摩擦、绳的质量和伸长都不计,绳子足够牢固,问:
(2010?南昌一模)如图所示,A,B两木块质量分别为4kg和1kg,C板的质量为5kg,A、C之间的动摩擦因数为0.25,桌面光滑,A、C静止时,将木块B由张紧状态抬高0.8m后释放,滑轮的摩擦、绳的质量和伸长都不计,绳子足够牢固,问: