题目内容
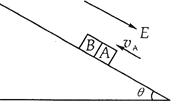
【题目】在倾角为θ的足够长的绝缘斜面上,带电的小物块A和不带电的绝缘小物块B正分别沿斜面向上滑行。斜面处于范围足够大的匀强电场中,场强方向平行斜面向下。当A刚追上B时,物块A的速度vA=1.8m/s,方向沿斜面向上,物块B的速度恰为零,如图所示。A追上B时发生第一次碰撞(碰撞过程经历时间极短,且无机械能损失,A的电荷也没有转移),碰后瞬间A的速度v1=0.6m/s,方向仍沿斜面向上;碰后经0.60s,物块A的速率变为v2=1.8m/s,在这0.60s时间内两物块没有再次相遇。已知物块A与斜面间的动摩擦因数μ=0.15,质量mA=0.5kg,物块B与斜面间的摩擦忽略不计,质量mB=0.25kg,匀强电场的场强![]() N/C,sinθ=0.6,cosθ=0.8,重力加速度g=10m/s2。求
N/C,sinθ=0.6,cosθ=0.8,重力加速度g=10m/s2。求
(1)第一次相碰后物块B的速率;
(2)物块A所带的电荷量;
(3)第一次相碰后0.60s内物块A的电势能的变化量.
【答案】(1)2.4 m/s(2)A带负电,电荷量为![]() (3)
(3)![]()
【解析】
(1)设碰后瞬间B的速度为vB,由于A与B碰撞无机械能损失,则:
![]() ,
,
代入数据解得 ![]() =2.4 m/s
=2.4 m/s
(2)碰后的0.6 s内,A的运动有两种可能:①一直加速向上;②减速向上再加速向下。
第①种情况:碰撞后物块B的加速度大小为![]() m/s2,方向沿斜面向下。
m/s2,方向沿斜面向下。
物块A的加速度大小为 ![]() m/s2
m/s2
设经![]() 时间第二次相遇,两物块位移相等,即
时间第二次相遇,两物块位移相等,即 ![]()
解得![]() =0.45 s <0.6 s,不合题意,所以A的运动只能是第②种情况。
=0.45 s <0.6 s,不合题意,所以A的运动只能是第②种情况。
以沿斜面向下的方向为正,设物块A碰撞后向上减速运动的加速度大小为a1,向下加速运动的加速度大小为a2,A受到的电场力为F,由题意得:![]()
分别对上滑和下滑过程运用牛顿第二定律列方程:
上滑过程 ![]() ,
,
下滑过程 ![]()
联立以上方程解得 F=—0.6 N(另解F=—3.4 N舍弃)、![]() m/s2、
m/s2、![]() m/s2。
m/s2。
F为负值,表明电场力沿斜面向上,由此可知物块A带负电,电荷量为![]() 。
。
(3)物块A上滑的位移大小为![]() m,
m,
下滑的位移大小为![]() m,
m,
故在0.60s时间内物块A的总位移为![]() m,方向向下。
m,方向向下。
电场力做功为:![]() J,
J,
物块A的电势能变化量![]() J
J

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案