题目内容
 如图是为了检验某种防护罩承受冲击能力的装置的一部分,M为半径为R=1.0m、固定于竖直平面内的四分之一光滑圆弧轨道,轨道上端切线水平,M的下端相切处置放竖直向上的弹簧枪,可发射速度不同的质量m=0.01kg的小钢珠,假设某次发射的钢珠沿轨道内侧恰好能经过M的上端点水平飞出,取g=10m/s2,弹簧枪的长度不计,则发射该钢珠前,弹簧的弹性势能为( )
如图是为了检验某种防护罩承受冲击能力的装置的一部分,M为半径为R=1.0m、固定于竖直平面内的四分之一光滑圆弧轨道,轨道上端切线水平,M的下端相切处置放竖直向上的弹簧枪,可发射速度不同的质量m=0.01kg的小钢珠,假设某次发射的钢珠沿轨道内侧恰好能经过M的上端点水平飞出,取g=10m/s2,弹簧枪的长度不计,则发射该钢珠前,弹簧的弹性势能为( )分析:在M轨道最高点,重力提供向心力,根据牛顿第二定律列方程求解最高点速度,然后根据机械能守恒定律列式求解;
解答:解:设钢珠在M轨道最高点的速度为v,在最高点,由题有:
mg=m
从发射前到最高点,由机械能守恒定律有:
EP=mgR+
mv2=0.15J
故选:B.
mg=m
| v2 |
| R |
从发射前到最高点,由机械能守恒定律有:
EP=mgR+
| 1 |
| 2 |
故选:B.
点评:根据重力恰好提供向心力求解出最高点速度是突破口,然后根据机械能守恒定律求解.

练习册系列答案
相关题目
 如图是为了检验某种防护罩承受冲击能力的装置,M为半径为R=1.0m、固定于竖直平面内的
如图是为了检验某种防护罩承受冲击能力的装置,M为半径为R=1.0m、固定于竖直平面内的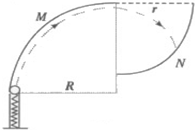 如图是为了检验某种防护罩承受冲击能力的装置,M为半径为R=1.0m、固定于竖直平面内的1/4光滑圆弧轨道,轨道上端切线水平,N为待检验的固定曲面,该曲面在竖直面内的截面为半径
如图是为了检验某种防护罩承受冲击能力的装置,M为半径为R=1.0m、固定于竖直平面内的1/4光滑圆弧轨道,轨道上端切线水平,N为待检验的固定曲面,该曲面在竖直面内的截面为半径 如图是为了检验某种防护罩承受冲击能力的实验装置,M是半径为R=1.0m、固定在竖直平面内的
如图是为了检验某种防护罩承受冲击能力的实验装置,M是半径为R=1.0m、固定在竖直平面内的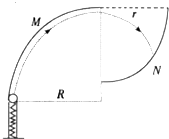 如图是为了检验某种防护罩承受冲击能力的装置,M为半径为R=1.0m、固定于竖直平面内的
如图是为了检验某种防护罩承受冲击能力的装置,M为半径为R=1.0m、固定于竖直平面内的