题目内容
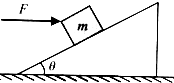
如图,一质量为m的滑块在水平力F的作用下能静止于倾角为θ的固定斜面上,则:
(1)若斜面光滑,F的大小应为多少?
(2)若滑块与斜面间的最大静摩擦力与滑动摩擦力相同,其动摩擦因数为μ(μ<tanθ且μ<
),F的取值范围是多少?
(1)若斜面光滑,F的大小应为多少?
(2)若滑块与斜面间的最大静摩擦力与滑动摩擦力相同,其动摩擦因数为μ(μ<tanθ且μ<
| 1 |
| tanθ |

(1)滑块受重力、支持力和推力,如图所示:
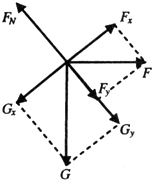
由平衡条件得:
即:
解方程,得到:F=mgtanθ;
(2)分析滑块受力情况,F的最小值Fmin对应静摩擦力沿斜面向上,并取最大值.
此时滑块受力如图所示:
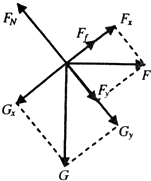
即:
解方程得到:Fmin=
mg
F的最大值Fmax对应静摩擦力沿斜面向下,并取最大值.
此时滑块受力如图所示
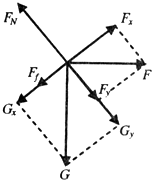
解得:
解方程得到:Fmax=
mg;
综上:
mg≤F≤
mg;
答:(1)若斜面光滑,F的大小应为mgtanθ;
(2)F的取值范围是:
mg≤F≤
mg.

由平衡条件得:
|
即:
|
解方程,得到:F=mgtanθ;
(2)分析滑块受力情况,F的最小值Fmin对应静摩擦力沿斜面向上,并取最大值.
此时滑块受力如图所示:

|
即:
|
解方程得到:Fmin=
| sinθ-μcosθ |
| cosθ+μsinθ |
F的最大值Fmax对应静摩擦力沿斜面向下,并取最大值.
此时滑块受力如图所示

|
解得:
|
解方程得到:Fmax=
| sinθ+μcosθ |
| cosθ-μsinθ |
综上:
| sinθ-μcosθ |
| cosθ+μsinθ |
| sinθ+μcosθ |
| cosθ-μsinθ |
答:(1)若斜面光滑,F的大小应为mgtanθ;
(2)F的取值范围是:
| sinθ-μcosθ |
| cosθ+μsinθ |
| sinθ+μcosθ |
| cosθ-μsinθ |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目







