��Ŀ����
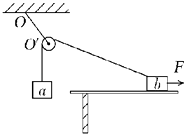
����Ŀ����ͼ��ʾ��һ���Ϊa�Ĺ̶�б���¶˹̶�һ���壬һ����ϵ��Ϊk���ᵯ���¶˹̶��ڵ����ϣ��ֽ�һ����Ϊm��С����б�����뵯���϶˾���Ϊs�����ɾ�ֹ�ͷţ���֪�����б���Ķ�Ħ������Ϊ�̣�����»������е������ΪEkm �� ��С�����ͷŵ��˶�����͵�Ĺ����У�����˵������ȷ���ǣ� ��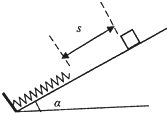
A.�̣�tana
B.�����뵯�ɽӴ���˲��ﵽ�����
C.���ɵ���������ܵ������������������ٵ�����������Ħ�������������֮��
D.���������뵯���϶�2s��б�洦�ɾ�ֹ�ͷţ����»����������������С��2Ekm
���𰸡�A,C,D
���������⣺A��С���Ӿ�ֹ�ͷź�����б���»������� mgsin������mgcos������� �̣�tan������A��ȷ��
B�������뵯�ɽӴ���˲�䣬���ɵĵ�����Ϊ�㣬����mgsin������mgcos�������������¼��٣����������������Դ�˲�䶯�ܲ���������ĺ���Ϊ��ʱ���ܲ����B����
C����������ת�����غ㶨��֪�����ɵ���������ܵ������������������ٵ��������������������֮������ܵ������˷�Ħ�����������ɵõ��ɵ���������ܵ������������������ٵ�����������Ħ�������������֮�ͣ���C��ȷ��
D�����������뵯���϶�2s��б�洦�ɾ�ֹ�ͷţ��»���������鶯������λ�ò��䣬�������ܲ��䣬��ΪEp����λ�õ��ɵ�ѹ����Ϊx��
���ݹ��ܹ�ϵ�ɵã�
�������뵯���϶�s��б�洦�ɾ�ֹ�ͷţ��»����������������Ϊ Ekm=mg��s+x��sin������mg��s+x��cos����Ep��
�������뵯���϶�s��б�洦�ɾ�ֹ�ͷţ��»����������������Ϊ Ekm��=mg��2s+x��sin������mg��2s+x��cos����Ep��
��2Ekm=mg��2s+2x��sin������mg��2s+2x��cos����2Ep=[mg��2s+x��sin������mg��2s+x��cos����Ep]+[mgxsin������mgxcos����Ep]=Ekm��+[mgxsin������mgxcos����Ep]
���������Ӵ����ɵ��������Ĺ����У�������������ת��Ϊ���ܺ����Ķ��ܣ�����ݹ��ܹ�ϵ�ɵã�mgxsin������mgxcos����Ep����mgxsin������mgxcos����Ep��0�����Ե�Ekm�䣼2Ekm����D��ȷ��
��ѡ��ACD
�����㾫�������ù��ܹ�ϵ�������غ㶨�ɶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1�������غ㶨�ɣ������Ȳ�������Ҳ���ᴴ������ֻ���һ����ʽת��Ϊ������ʽ�����ߴ�һ������ת�Ƶ���һ�����壬����ת����ת�ƹ����У��������������ֲ��䣮