题目内容
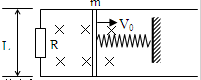
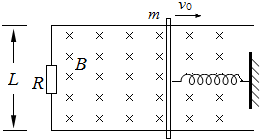
 如图所示,固定的水平光滑金属导轨,间距为L,左端接有阻值为R的电阻,处在方向竖直、磁感应强度为B的匀强磁场中,质量为m的导体棒与固定弹簧相连,放在导轨上,导轨与导体棒的电阻均可忽略.初始时刻,弹簧恰处于自然长度,导体棒具有水平向右的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.
如图所示,固定的水平光滑金属导轨,间距为L,左端接有阻值为R的电阻,处在方向竖直、磁感应强度为B的匀强磁场中,质量为m的导体棒与固定弹簧相连,放在导轨上,导轨与导体棒的电阻均可忽略.初始时刻,弹簧恰处于自然长度,导体棒具有水平向右的初速度v0.在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.(1)求初始时刻导体棒受到的安培力.
(2)若导体棒从初始时刻到速度第一次为零时,弹簧的弹性势能为Ep,则这一过程中安培力所做的功W1和电阻R上产生的焦耳热Q1分别为多少?导体棒往复运动,最终将静止于何处?从导体棒开始运动直到最终静止的过程中,电阻R上产生的焦耳热Q为多少?
分析:(1)由欧姆定律、安培力公式和感应电动势知识推导安培力.
(2)导体棒向右运动时,弹力和安培力对棒做功根据功能关系求出安培力所做的功W1和电阻R上产生的焦耳热Q1.运用能量转化及平衡条件等求出电阻R上产生的焦耳热Q.
(2)导体棒向右运动时,弹力和安培力对棒做功根据功能关系求出安培力所做的功W1和电阻R上产生的焦耳热Q1.运用能量转化及平衡条件等求出电阻R上产生的焦耳热Q.
解答:解:(1)初始时刻棒中感应电动势:E=BLυ0
棒中感应电流:I=
作用于棒上的安培力:F=BIL
联立得:F=
,安培力方向水平向左
(2)设安培力做功为W1.弹力做功为W弹.
由动能定理得:W1+W弹=0-
m
又-W1=Q1,-W弹=Ep
解得电阻R上产生的焦耳热为:Q1=
mυ02-EP
(3)由能量转化及平衡条件等判断:棒最终静止于初始位置(弹簧原长处)
由能量转化和守恒得:Q=
mυ02
答:(1)初始时刻导体棒受到的安培力大小为
,方向水平向左;
(2)安培力所做的功W1等于EP-
mυ02,电阻R上产生的焦耳热Q1等于
mυ02-EP.导体棒往复运动,最终静止于初始位置(弹簧原长处).从导体棒开始运动直到最终静止的过程中,电阻R上产生的焦耳热Q为
mυ02.
棒中感应电流:I=
| E |
| R |
作用于棒上的安培力:F=BIL
联立得:F=
| B2L2v0 |
| R |
(2)设安培力做功为W1.弹力做功为W弹.
由动能定理得:W1+W弹=0-
| 1 |
| 2 |
| v | 2 0 |
又-W1=Q1,-W弹=Ep
解得电阻R上产生的焦耳热为:Q1=
| 1 |
| 2 |
(3)由能量转化及平衡条件等判断:棒最终静止于初始位置(弹簧原长处)
由能量转化和守恒得:Q=
| 1 |
| 2 |
答:(1)初始时刻导体棒受到的安培力大小为
| B2L2v0 |
| R |
(2)安培力所做的功W1等于EP-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:弄清运动过程中能量如何转化,并应用能量转化和守恒定律分析解决问题是此题关键.

练习册系列答案
相关题目
 (2005?江苏)如图所示,固定的水平光滑金属导轨,间距为L,左端接有阻值为R的电阻,处在方向竖直、磁感应强度为B的匀强磁场中,质量为m的导体棒与固定弹簧相连,放在导轨上,导轨与导体棒的电阻均可忽略,初始时刻,弹簧恰处于自然长度,导体棒具有水平向右的初速度υ0,在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触.
(2005?江苏)如图所示,固定的水平光滑金属导轨,间距为L,左端接有阻值为R的电阻,处在方向竖直、磁感应强度为B的匀强磁场中,质量为m的导体棒与固定弹簧相连,放在导轨上,导轨与导体棒的电阻均可忽略,初始时刻,弹簧恰处于自然长度,导体棒具有水平向右的初速度υ0,在沿导轨往复运动的过程中,导体棒始终与导轨垂直并保持良好接触. (2011?江苏)如图所示,固定的水平长直导线中通有电流I,矩形线框与导线在同一竖直平面内,且一边与导线平行.线框由静止释放,在下落过程中( )
(2011?江苏)如图所示,固定的水平长直导线中通有电流I,矩形线框与导线在同一竖直平面内,且一边与导线平行.线框由静止释放,在下落过程中( )