题目内容
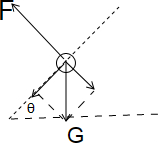
 如图所示,小车在斜面上沿斜面向下运动,当小车以不同的加速度运动时,系在小车顶部的小球分别如图中①②③所示三种状态.
如图所示,小车在斜面上沿斜面向下运动,当小车以不同的加速度运动时,系在小车顶部的小球分别如图中①②③所示三种状态.①中细线呈竖直方向,②中细线垂直斜面,③中细线水平.试分别求出上述三种状态中小车的加速度.(斜面倾角为θ)
分析:本题的突破口是:小车沿斜面加速下滑,故物体的加速度沿斜面方向,所以小球所受的合力沿斜面方向向下,这样就可求出小球所受的合外力从而求出物体加速度的大小.
解答:解:①中细线呈竖直方向,小球受重力和竖直向上的拉力,二力平衡,故小车的加速度为零
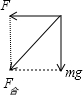
②中细线垂直斜面以小球为研究对象,其受力如图所示
由牛顿第二定律得:a=
=gsinθ
方向:沿斜面竖直向下
③中细线水平以小球为研究对象,其受力如图所示,
由于F合沿斜面方向,故有tanθ=
所以摆线的拉力F=
=mgctgθ
又sinθ=
故a=
方向沿斜面向下
答:①中细线呈竖直方向,②中细线垂直斜面,③中细线水平三种状态下,小车的加速度分别为①a=0 ②a=gsinθ,方向沿斜面向下 ③a=
,方向沿斜面向下.
②中细线垂直斜面以小球为研究对象,其受力如图所示

由牛顿第二定律得:a=
| mgsinθ |
| m |
方向:沿斜面竖直向下
③中细线水平以小球为研究对象,其受力如图所示,

由于F合沿斜面方向,故有tanθ=
| mg |
| F |
所以摆线的拉力F=
| mg |
| tanθ |
又sinθ=
| mg |
| ma |
| g |
| sinθ |
答:①中细线呈竖直方向,②中细线垂直斜面,③中细线水平三种状态下,小车的加速度分别为①a=0 ②a=gsinθ,方向沿斜面向下 ③a=
| g |
| sinθ |
点评:小车只能沿斜面加速下滑,故小车的加速度沿斜面方向,所以小球的加速度也沿斜面方向,即小球所受的合外力沿斜面方向,重力大小方向已知,这样就知道了合力的方向和大小,从而求出绳子的拉力和小球的加速度.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
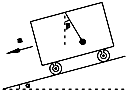 如图所示,小车在倾角为α的斜面上匀加速运动,车厢顶用细绳悬挂一小球,发现悬绳与竖直方向形成一个稳定的夹角β,则小车的加速度大小是
如图所示,小车在倾角为α的斜面上匀加速运动,车厢顶用细绳悬挂一小球,发现悬绳与竖直方向形成一个稳定的夹角β,则小车的加速度大小是
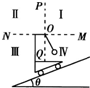 如图所示,小车在外力作用下沿倾角为θ的斜面做直线运动,小车的支架上用细线拴一个摆球,悬点为0,现用水平虚线MN和竖直虚线PQ将竖直平面空间分成四个区间,则下列说法正确的是( )
如图所示,小车在外力作用下沿倾角为θ的斜面做直线运动,小车的支架上用细线拴一个摆球,悬点为0,现用水平虚线MN和竖直虚线PQ将竖直平面空间分成四个区间,则下列说法正确的是( )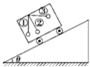 如图所示,小车在斜面上沿斜面向下运动,当小车以不同的加速度运动时,系在小车顶部的小球分别如图中①②③所示三种状态.
如图所示,小车在斜面上沿斜面向下运动,当小车以不同的加速度运动时,系在小车顶部的小球分别如图中①②③所示三种状态.