Question

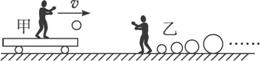
甲、乙两人做抛球游戏，如图16-4-8所示，甲站在一辆平板车上，车与水平地面间的摩擦不计，甲与车的总质量M=10 kg，另有一质量m=2 kg的球，乙站在车的对面的地上身旁有若干质量不等的球.开始车静止，甲将球以速度v（相对于地面）水平抛给乙，乙接到抛来的球后，马上将另一只质量为m′=2m的球以相同的速度v水平抛回给甲，甲接到后，再以相同速度v将此球抛给乙，这样反复进行，乙每次抛回给甲的球的质量都等于他接到球的质量的2倍，求：

（1）甲第二次抛出球后，车的速度的大小.

（2）从第一次算起，甲抛出多少个球，再不能接到乙抛回来的球.

图16-4-8

Answer 1

（1）  向左  （2）抛出5个球后再接不到球

解析:

（1）以甲和车及第一个球为系统，选向右为正方向，设甲第一次抛出球后的后退速度为v₁，由动量守恒得0=mv-Mv₁                                             ①

再以甲和车及抛回来的球为系统，设甲第二次抛球的速度为v₂，甲接到一个从右方抛过来的质量为2m的球，接着又向右扔回一个质量为2m的球，此过程应用动量守恒得

-Mv₁-2mv=-Mv₂+2mv                                                          ②

整理①②式得Mv₂=2²mv+Mv₁

解出v₂=，方向向左.

（2）依上次的分析推理可得Mv₁=mv                                           ③

……

Mv_n=2ⁿmv+Mv_n-1                                                             ④

v_n=(2ⁿ+2^n-1+……+2²+1)                                                    ⑤

要使甲接不到乙抛回来的球，必须有v_n＞v

即(2ⁿ+2^n-1+……+2²+1)＞1

解得n＞4，故甲抛出5个球后，再也接不到乙抛回来的球.