��Ŀ����
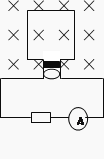
����Ŀ����ͼ��ʾ���⻬��ˮƽ������һ����M=9kg��ľ�壬���Ҷ�ǡ�ú� ![]() �⻬�̶��������AB�ĵ˵ȸ߶Խӣ�ľ���ˮƽ�ϱ�����Բ��������У���ľ���Ҷ˷���һ����m0=2kg������C������Ϊ�ʵ㣩����֪Բ������뾶R=0.9m���ֽ�һ����m=4kg��С���飨����Ϊ�ʵ㣩���ɹ������A�������ͷţ����黬��B�˺����ľ�壬����ľ���Ҷ˵�����Cճ��һ����ľ�������У����ǡ�ò���ľ����˻�������֪������ľ���ϱ���Ķ�Ħ��������1=0.25������C��ľ���ϱ���Ķ�Ħ��������2=0.1��ȡg=10m/s2 �� ��
�⻬�̶��������AB�ĵ˵ȸ߶Խӣ�ľ���ˮƽ�ϱ�����Բ��������У���ľ���Ҷ˷���һ����m0=2kg������C������Ϊ�ʵ㣩����֪Բ������뾶R=0.9m���ֽ�һ����m=4kg��С���飨����Ϊ�ʵ㣩���ɹ������A�������ͷţ����黬��B�˺����ľ�壬����ľ���Ҷ˵�����Cճ��һ����ľ�������У����ǡ�ò���ľ����˻�������֪������ľ���ϱ���Ķ�Ħ��������1=0.25������C��ľ���ϱ���Ķ�Ħ��������2=0.1��ȡg=10m/s2 �� ��
��1�����鵽��Բ����B��ʱ�����������֧������СFN ��
��2��ľ��ij���l��
���𰸡�
��1��
�⣺�����A���»���B�ˣ��ɻ�е���غ�ã�
mgR= ![]()
�ã� ![]() =
= ![]() =
= ![]() m/s
m/s
��B�㣬��ţ�ٵڶ����ɵã�FN��mg=m ![]()
��ù���Ի����֧����Ϊ��FN=3 mg=3��4��10=120 N
��ţ�ٵ������ɿ�֪������Թ����ѹ��Ϊ120 N
��2��
�⣺���黬��ľ�������ľ���Ҳ������C������ײ��������Ϊ����������ײ��ͬ���ٶ�Ϊv1����
mv0=��m+m0��v1
�������ݵã� ![]() m/s
m/s
�Ի��顢���C�Լ�ľ�壬������ɵ�ϵͳ��ˮƽ����Ķ����غ㣬��ĩ�ٶ�Ϊv2���ɶ����غ��У�
��m+m0��v1=��m+m0+M��v2��
���ܵ�ת�����غ�ã�����1m+��2m0��gl= ![]()
�������ݵã�l=1.2m
����������1�����ݻ�е���غ����С�����A���˶���B����ٶȣ�����ţ�ٵڶ�����������������֧��������2�����黬��ľ���ľ�����ȼ���ֱ���˶����������ȼ���ֱ���˶����������ٶ����ʱ��һ��������ֱ���˶�������ϵͳ�Ķ����غ㣬����ٶ����ʱ�Ĺ�ͬ�ٶȣ��������غ㶨�ɶ�ϵͳ�о���ʽ�����ľ��ij���l��
�����㾫����������Ŀ����֪���������ù��ܹ�ϵ�Ͷ����غ㶨�ɵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���յ�ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1�������غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�