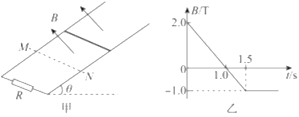
��Ŀ����
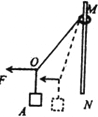
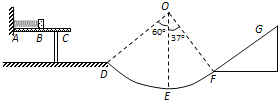
����Ŀ����ͼ��ʾ��ACΪ�⻬��ˮƽ���棬�ᵯ�ɵ�һ�˹̶���A�˵���ֱǽ����![]() ����
����![]() ��С��齫���ɵ���һ��ѹ����B�㣬֮���ɾ�ֹ�ͷţ��뿪���ɺ��C��ˮƽ�ɳ���ǡ�ô�D����
��С��齫���ɵ���һ��ѹ����B�㣬֮���ɾ�ֹ�ͷţ��뿪���ɺ��C��ˮƽ�ɳ���ǡ�ô�D����![]() ���ٶ������߷��������ֱ���ڵĹ⻬Բ�����
���ٶ������߷��������ֱ���ڵĹ⻬Բ�����![]() С��������������ײ
С��������������ײ![]() ΪԲ�������Բ�ģ�EΪԲ���������͵㣬Բ������İ뾶
ΪԲ�������Բ�ģ�EΪԲ���������͵㣬Բ������İ뾶![]() ��
��![]() ��
��![]() С����˶���F������㹻����б��FG��б��FG��Բ���������F�㣬С������б���Ķ�Ħ������
С����˶���F������㹻����б��FG��б��FG��Բ���������F�㣬С������б���Ķ�Ħ������![]() ��
��![]() ��ȡ
��ȡ![]() ���ƿ�������
���ƿ�������![]() ��
��
��1������������еĵ������ܣ�
��2��С����һ�ε���Բ�������E��ʱ��Բ�������ѹ����С��
��3���ж�С�����б��FG��һ�η���Բ��������ܷ�ص�Բ�������D�㣿���ܣ����С���ص�D����ٶȣ������ܣ���⾭���㹻����ʱ���С���ͨ��Բ�������͵�E���ٶȴ�С��
���𰸡�![]() ��
��![]() 30N��
30N��![]() 2
2![]() ��
��
��������
��1����С�����C����ٶ�Ϊ![]() ������D���У�
������D����![]()
�赯��������еĵ�������Ϊ![]() ����
����![]()
��������������ã�![]() ��
��
![]() ��С�����E����ٶ�Ϊ
��С�����E����ٶ�Ϊ![]() �����D��E�Ĺ������У�
�����D��E�Ĺ������У�
![]()
����E�㣬Բ�����С����֧����ΪN�����У�![]()
�������ݽ�ã�![]() ��
��![]()
��ţ�ٵ������ɿ�֪��С��鵽��Բ�����E��ʱ��Բ�����ѹ��Ϊ30![]()
![]() ��С������б��FG�ϻ���������Ϊx����E��������Ĺ������У�
��С������б��FG�ϻ���������Ϊx����E��������Ĺ������У�
![]()
С�����һ����б���ϻ�������F�Ĺ��̿˷�Ħ�������Ĺ�Ϊ![]() ����
����
![]()
С������D��Ķ���Ϊ![]() ����
����![]()
�������ݽ�ã�![]() ��
��![]() ��
��![]()
��Ϊ![]() ����С���岻�ܷ���D��
����С���岻�ܷ���D��![]()
С�������ս���F������ڹ�Բ���Բ�ĵ���ֱ�߶ԳƵĵ�֮���������˶���С����Ļ�е���غ㣬����������͵���ٶ�Ϊ![]() �����У�
������
![]()
�������ݽ�ã�![]()
��![]() ����������еĵ�������Ϊ
����������еĵ�������Ϊ![]() ��
��
![]() С����һ�ε���Բ�������E��ʱ��Բ�������ѹ����С��30N��
С����һ�ε���Բ�������E��ʱ��Բ�������ѹ����С��30N��
![]() С�����б��FG��һ�η���Բ��������ܻص�Բ�������D��
С�����б��FG��һ�η���Բ��������ܻص�Բ�������D��![]() �����㹻����ʱ���С���ͨ��Բ�������͵�E���ٶȴ�СΪ2
�����㹻����ʱ���С���ͨ��Բ�������͵�E���ٶȴ�СΪ2![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�