题目内容
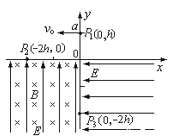
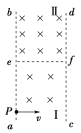
【题目】如图所示,aefc和befd是垂直于纸面向里的匀强磁场Ⅰ、Ⅱ的边界。磁场Ⅰ、Ⅱ的磁感应强度分别为B1、B2,且B2=2B1,其中bc=ea=ef.一质量为m、电荷量为q的带电粒子垂直边界ae从P点射入磁场Ⅰ,后经f点进入磁场 Ⅱ,并最终从fc边界射出磁场区域。不计粒子重力,该带电粒子在磁场中运动的总时间为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
粒子在磁场中运动只受洛伦兹力作用,故粒子做圆周运动,洛伦兹力做向心力,故有
![]()
所以
![]()
粒子垂直边界ae从P点射入磁场Ⅰ,后经f点进入磁场Ⅱ,故根据几何关系可得:粒子在磁场Ⅰ中做圆周运动的半径为磁场宽度d;根据轨道半径表达式,由两磁场区域磁感应强度大小关系可得:粒子在磁场Ⅱ中做圆周运动的半径为磁场宽度![]() ,那么,根据几何关系可得:粒子从P到f转过的中心角为
,那么,根据几何关系可得:粒子从P到f转过的中心角为![]() ,粒子在f点沿fd方向进入磁场Ⅱ;然后粒子在磁场Ⅱ中转过
,粒子在f点沿fd方向进入磁场Ⅱ;然后粒子在磁场Ⅱ中转过![]() 在e点沿ea方向进入磁场Ⅰ;最后,粒子在磁场Ⅰ中转过
在e点沿ea方向进入磁场Ⅰ;最后,粒子在磁场Ⅰ中转过![]() 后从fc边界射出磁场区域;故粒子在两个磁场区域分别转过
后从fc边界射出磁场区域;故粒子在两个磁场区域分别转过![]() ,根据周期
,根据周期
![]()
可得:该带电粒子在磁场中运动的总时间为
![]()
故选B。

练习册系列答案
相关题目