题目内容
【题目】如图，带电粒子垂直电场线方向进入有界匀强电场，从Q点飞出时又进入有界的匀强磁场，并从D点离开磁场且落在了荧光屏的ON区域。已知：电场方向沿纸面竖直向上、宽度为d，P、Q两点在竖直方向上的距离为d；QD为磁场的水平分界线，上方磁场垂直纸面向外、下方磁场垂直纸向里、磁感应强度大小相同，磁场宽度为d；粒子质量为m、带电量为q，不计重力，进入电场的速度为v0。
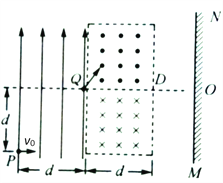
（1）求电场强度E的大小；
（2）大致画出粒子以最大半径穿过磁场的运动轨迹
（3）求磁感应强度的最小值B。
【答案】（1）
（2）
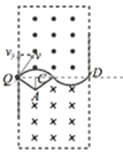（3）
【解析】带电粒子在电场中做类平抛运动，根据平抛运动的基本公式求解即可；粒子在磁场中做匀速圆周运动，画出轨迹；粒子以最大半径穿过磁场时，对应的磁感应强度最小，粒子在磁场中，根据牛顿第二定律列式结合几何关系即可求。
（1）带电粒子在电场中做类平抛运动，设电场强度为E，运动时间为t，运动的加速度为a，则有：
，
粒子在电场中，根据牛顿第二定律得：
解得：
（2）粒子以最大半径穿过磁场的运动轨迹如图所示
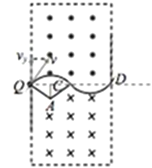
（3）粒子以最大半径穿过磁场时，对应的磁感应强度最小，设其值为B，如图，设在Q点时的速度为v，沿电场方向的分速度为vy，进入磁场后粒子做圆周运动的轨道半径为r，粒子在磁场中，根据牛顿第二定律得：
由几何关系得：
则
又粒子在电场中：
得
练习册系列答案
习题精选系列答案
相关题目
