题目内容
16. 假设某宇航员乘坐探月卫星登上月球,在月球的一个山坡上水平抛出一个小球,落到山坡上一个低洼处,如图所示,已知抛出点与落地点之间的高度差为h,抛出点与落地点之间的连线与水平面之间的夹角为θ,月球上重力加速度是地球表面重力加速度g的$\frac{1}{6}$,求:
假设某宇航员乘坐探月卫星登上月球,在月球的一个山坡上水平抛出一个小球,落到山坡上一个低洼处,如图所示,已知抛出点与落地点之间的高度差为h,抛出点与落地点之间的连线与水平面之间的夹角为θ,月球上重力加速度是地球表面重力加速度g的$\frac{1}{6}$,求:(1)小球在空中的飞行时间;
(2)小球抛出时的速度大小.
分析 根据高度,结合位移时间公式求出小球在空中飞行的时间,根据水平位移和时间求出小球抛出时的速度大小.
解答 解:(1)根据h=$\frac{1}{2}•\frac{1}{6}g{t}^{2}$得,t=$\sqrt{\frac{12h}{g}}$.
(2)根据x=v0t得,$\frac{h}{tanθ}={v}_{0}\sqrt{\frac{12h}{g}}$,
解得${v}_{0}=\frac{1}{tanθ}\sqrt{\frac{gh}{12}}$.
答:(1)小球在空中的飞行时间为$\sqrt{\frac{12h}{g}}$;
(2)小球抛出时的速度大小为$\frac{1}{tanθ}\sqrt{\frac{gh}{12}}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解.

练习册系列答案
相关题目
6.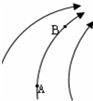 如图所示,为某个电场中的部分电场线,A、B两点的电势分别记为φA、φB,A、B两点的电场强度分别记为EA、EB,则( )
如图所示,为某个电场中的部分电场线,A、B两点的电势分别记为φA、φB,A、B两点的电场强度分别记为EA、EB,则( )
 如图所示,为某个电场中的部分电场线,A、B两点的电势分别记为φA、φB,A、B两点的电场强度分别记为EA、EB,则( )
如图所示,为某个电场中的部分电场线,A、B两点的电势分别记为φA、φB,A、B两点的电场强度分别记为EA、EB,则( )| A. | φA>φB、EA>EB | B. | φA<φB、E A<EB | C. | φA>φB、EA<EB | D. | φA<φB、E A>EB |
7.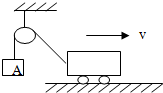 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度V匀速向右运动时,物体A的速度情况是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度V匀速向右运动时,物体A的速度情况是( )
 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度V匀速向右运动时,物体A的速度情况是( )
如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度V匀速向右运动时,物体A的速度情况是( )| A. | 物体的速度始终大于V | B. | 物体的速度始终等于V | ||
| C. | 物体的速度始终小于V | D. | 物体的速度先大于V后变小于V |
11.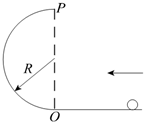 如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力,下列说法正确的是( )
如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力,下列说法正确的是( )
 如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力,下列说法正确的是( )
如图所示,小球沿水平面通过O点进入半径为R的半圆弧轨道后恰能通过最高点P,然后落回水平面.不计一切阻力,下列说法正确的是( )| A. | 小球落地点离O点的水平距离为R | |
| B. | 小球落地点离O点的水平距离为2R | |
| C. | 小球落地点离O点的水平距离为3R | |
| D. | 小球运动到半圆弧最高点P时向心力恰好为零 |
1.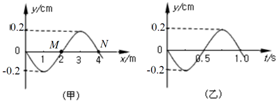 一列横波沿x轴正方向传播,图(甲)为t=0.5s时的波动图象,图(乙)为介质中某质点的振动图象.对该波的说法正确的是( )
一列横波沿x轴正方向传播,图(甲)为t=0.5s时的波动图象,图(乙)为介质中某质点的振动图象.对该波的说法正确的是( )
 一列横波沿x轴正方向传播,图(甲)为t=0.5s时的波动图象,图(乙)为介质中某质点的振动图象.对该波的说法正确的是( )
一列横波沿x轴正方向传播,图(甲)为t=0.5s时的波动图象,图(乙)为介质中某质点的振动图象.对该波的说法正确的是( )| A. | 乙图描述的是甲图中M点的振动情况 | |
| B. | 这列机械波的频率为0.25Hz | |
| C. | t=0.5s时质点N的位移为0,振幅为0 | |
| D. | 这列机械波的波速为4m/s |
5.下列实验、原理和相应的发明对应完全正确的是( )
| A. | 奥斯特实验--电磁铁 | |
| B. | 电磁感应--电动机 | |
| C. | 磁场对电流的作用--发电机 | |
| D. | 麦克斯韦的电磁场理论--无线电通讯 |