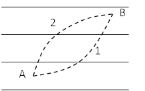Question

【题目】在长期的科学实践中，人类已经建立起各种形式的能量概念及其量度的方法，其中一种能量是势能。势能是由于各物体间存在相互作用而具有的、由各物体间相对位置决定的能。如重力势能、弹性势能、分子势能、电势能等。

（1）如图1所示，内壁光滑、半径为R的半圆形碗固定在水平面上，将一个质量为m的小球（可视为质点）放在碗底的中心位置C处。现给小球一个水平初速度v0（v0<），使小球在碗中一定范围内来回运动。已知重力加速度为g。

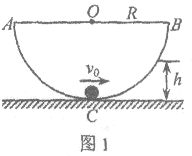
a. 若以AB为零势能参考平面，写出小球在最低位置C处的机械能E的表达式；

b. 求小球能到达的最大高度h；说明小球在碗中的运动范围，并在图1中标出。

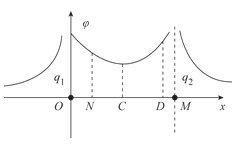
（2）如图2所示，a、b为某种物质的两个分子，以a为原点，沿两分子连线建立x轴。如果选取两个分子相距无穷远时的势能为零，则作出的两个分子之间的势能EP与它们之间距离x的EP-x关系图线如图3所示。

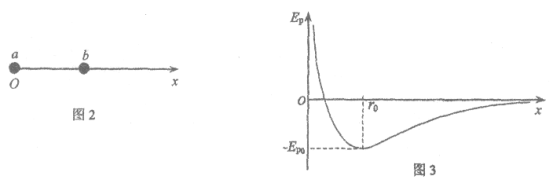
假设分子a固定不动，分子b只在ab间分子力的作用下运动（在x轴上）。当两分子间距离为r0时，b分子的动能为EK0（EK0<EP0）。求a、b分子间的最大势能EPm；并利用图3，结合画图说明分子b在x轴上的运动范围。

Answer 1

【答案】（1）a.；b.（2）△x=x2-x1；

【解析】

（1）a.小球的机械能

b.以水平面为零势能参考平面

根据机械能守恒定律

解得

小球在碗中的M与N之间来回运动，M与N等高，如图所示。

（2）当b分子速度为零时，此时两分子间势能最大根据能量守恒，有

由图线可知，当两分子间势能为时，b分子对应和两个位置坐标，b分子的活动范围

△x=x2-x1

如图所示。