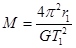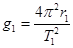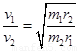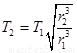题目内容
为了探测某星球，载着登陆舱的探测飞船在以该星球中心为圆心，半径为r1的圆轨道上运动，周期为T1，总质量为m1，随后登陆舱脱离飞船，变轨到离星球更近的半径为r2的圆轨道上运动，登陆舱的质量为m2，则（ ）
A．该星球的质量为M=
| ||||||||
B．该星球表面的重力加速度为g1=
| ||||||||
C．登陆舱在半径为r1与半径为r2的轨道上运动时的速度大小之比为
| ||||||||
D．登陆舱在半径为r2的轨道上做圆周运动的周期为T2=T1
|
A、研究飞船绕星球做匀速圆周运动，根据万有引力提供向心力，列出等式：
=m1
r1
得出：M=
，故A错误；
B、根据圆周运动知识，a=
只能表示在半径为r1的圆轨道上向心加速度，而不等于X星球表面的重力加速度，故B错误．
C、研究登陆舱绕星球做匀速圆周运动，根据万有引力提供向心力有：
在半径为r的圆轨道上运动：
=
得出：v=
表达式里M为中心体星球的质量，R为运动的轨道半径．
所以登陆舱在r1与r2轨道上运动时的速度大小之比为
=
，故C错误．
D、研究登陆舱绕星球做匀速圆周运动，根据万有引力提供向心力，列出等式：
在半径为r的圆轨道上运动：
=
得出：T=2π
．
表达式里M为中心体星球的质量，R为运动的轨道半径．所以登陆舱在r1与r2轨道上运动时的周期大小之比为：
=
所以：T2=T1
，故D正确．
故选：D．
| GMm1 |
| r1 |
| 4π2 | ||
|
得出：M=
4π2
| ||
G
|
B、根据圆周运动知识，a=
| 4π2r1 | ||
|
C、研究登陆舱绕星球做匀速圆周运动，根据万有引力提供向心力有：
在半径为r的圆轨道上运动：
| GMm |
| R2 |
| mv2 |
| R |
|
所以登陆舱在r1与r2轨道上运动时的速度大小之比为
| v1 |
| v2 |
|
D、研究登陆舱绕星球做匀速圆周运动，根据万有引力提供向心力，列出等式：
在半径为r的圆轨道上运动：
| GMm |
| R2 |
| m4π2r |
| T2 |
|
表达式里M为中心体星球的质量，R为运动的轨道半径．所以登陆舱在r1与r2轨道上运动时的周期大小之比为：
| T1 |
| T2 |
|
所以：T2=T1
|
故选：D．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
