题目内容
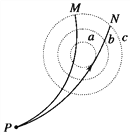
【题目】如图所示,在绝缘光滑的水平面上,建立一平面直角坐标系xoy,整个空间有一垂直水平面向下的匀强磁场B=0.10T。在y轴正半轴3.0m到9.0m之间有一厚度不计的固定弹性绝缘板。在原点O处静止一个质量m1=2.0×10-4kg,带正电,电量为q=1.0×10-2C的物体。在x轴负半轴某一位置有一个m2=3.0×10-4kg的不带电物体,以一定速率沿x轴向正方向运动并与m1物体发生碰撞并粘在一起。两物体都作为质点处理,碰撞时没有电量损失。求:(1)若m2的速率v0=5.0m/s,则碰后粘在一起系统损失的动能是多少?(2)若两物体粘在一起后,先与绝缘板发生一次碰撞后经过坐标为x=-3.0m,y=9.0m的位置P,则m2与m1相碰前的速率v是多少?(与绝缘板碰撞没有能量和电量损失)
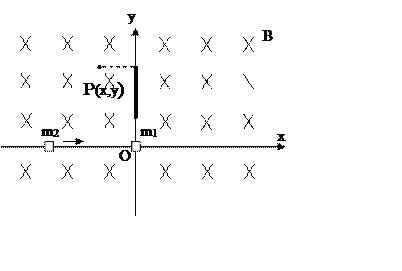
【答案】(1)1.5×10-3J (2)10m/s 12.5m/s
【解析】(1)水平方向不受外力由动量守恒有: ![]() ,
,
由能量关系有: ![]() ,
,
联立解得: ![]() ;
;
(2)水平方向不受外力由动量守恒有: ![]() ,
,
在洛伦兹力作用下做匀速圆周运动由牛顿第二定律有: ![]() ,
,
由几何关系有: ![]() ,
, ![]() ,
,
解得: ![]() ;
; ![]() .
.

练习册系列答案
相关题目