题目内容
如图所示,一细长的圆柱形均匀玻璃棒,其一个端面是平面(垂直于轴线),另一个端面是球面,球心位于轴线上。现有一很细的光束沿平行于轴线方向且很靠近轴线入射。当光从平端面射入棒内时,光线从另一端面射出后与轴线的交点到球面的距离为a;当光线从球形端面射入棒内时,光线在棒内与轴线的交点到球面的距离为b。试近似地求出玻璃的折射率n。

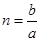
本题考查几何光学,首先画出光路图,由几何关系求解
入射的两条光线如图所示。α1、β1是从平端入射的光线通过球形端面时的入射角和折射角;α2、β2是从球形端面入射的光线通过球面时的入射角和折射角。根据折射定律有
nsinα1=sinβ1 (1)
sinα2=nsinβ2 (2)
由几何关系有β1=α1+δ1 (3)
α2=β2+δ2 (4)
设球面的半径为R,注意到α1、α2、δ1、δ2都是小角度,故有Rα1=aδ1 (5)
Rα2=bδ2 (6)
根据题给的条件,(1)、(2)式可近似表示成nα1=β1 (7)
α2=nβ2 (8)
由(3)式?(8)式得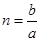 (9)
(9)
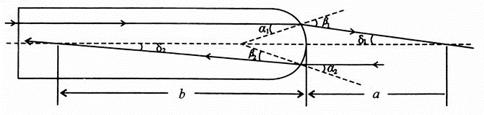
入射的两条光线如图所示。α1、β1是从平端入射的光线通过球形端面时的入射角和折射角;α2、β2是从球形端面入射的光线通过球面时的入射角和折射角。根据折射定律有
nsinα1=sinβ1 (1)
sinα2=nsinβ2 (2)
由几何关系有β1=α1+δ1 (3)
α2=β2+δ2 (4)
设球面的半径为R,注意到α1、α2、δ1、δ2都是小角度,故有Rα1=aδ1 (5)
Rα2=bδ2 (6)
根据题给的条件,(1)、(2)式可近似表示成nα1=β1 (7)
α2=nβ2 (8)
由(3)式?(8)式得
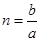 (9)
(9)

练习册系列答案
相关题目
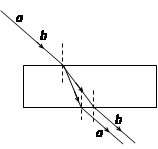
 光传播时,若遇到的障碍物的尺寸比光的波长大很多,衍射现象十分明显,此时不能认为光沿直线传播
光传播时,若遇到的障碍物的尺寸比光的波长大很多,衍射现象十分明显,此时不能认为光沿直线传播 在太阳光照射下,水面上油膜出现彩色花纹是光的衍射现象
在太阳光照射下,水面上油膜出现彩色花纹是光的衍射现象 光导纤维丝内芯材料的折射率比外套材料的折射率大
光导纤维丝内芯材料的折射率比外套材料的折射率大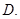 雨后天边的七色彩虹是光的色散现象
雨后天边的七色彩虹是光的色散现象
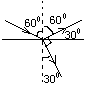
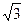 的玻璃射入空气中,折射角是多大?画出光路图。
的玻璃射入空气中,折射角是多大?画出光路图。