题目内容
11.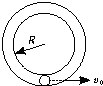 如图所示,一半径为R的光滑圆形细管,固定于竖直平面内,放置于管内最低处的小球以初速度v0沿管内运动,欲使小球能通过管的最高点,且小球在最高点时对管壁有向下的压力,v0必须满足的条件是( )
如图所示,一半径为R的光滑圆形细管,固定于竖直平面内,放置于管内最低处的小球以初速度v0沿管内运动,欲使小球能通过管的最高点,且小球在最高点时对管壁有向下的压力,v0必须满足的条件是( )| A. | v0≤2$\sqrt{Rg}$ | B. | v0≥$\sqrt{5Rg}$ | C. | v0≤2$\sqrt{Rg}$或v0≥$\sqrt{5Rg}$ | D. | 2$\sqrt{Rg}$≤v0≤$\sqrt{5Rg}$ |
分析 若小球在最高点时对管壁有向下的压力,则管壁对小球有向上的支持力,则小球所受重力和支持力的合力提供向心力,小球的速度再根据从最低点到最高点的过程中,只有重力做功,由机械能守恒即可求解范围
解答 解:在最高点小球的重力和管壁对小球的支持力提供向心力,
则mg-T=$m\frac{{v}^{2}}{R}$,
当T=0时,速度最大,
解得:v=$\sqrt{gR}$
所以当0≤v<$\sqrt{gR}$时,小球在最高点时对管壁有向下的压力,
从最低点到最高点的过程中,只有重力做功,由机械能守恒得:
$\frac{1}{2}$mv02=mg•2R+$\frac{1}{2}$mv2
当v=0时,解得:${v}_{0}=\sqrt{2gR}$,
当v=$\sqrt{gR}$时,解得:${v}_{0}=\sqrt{5gR}$
所以v0的范围为:2$\sqrt{Rg}$≤v0≤$\sqrt{5Rg}$,故D正确.
故选:D
点评 本题主要考查了机械能守恒定律、圆周运动向心力公式的直接应用,难度适中.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
1.阴极射线管电视机的玻璃荧光屏表面经常有许多灰尘,这主要是因为( )
| A. | 灰尘的自然堆积 | |
| B. | 玻璃有较强的吸附灰尘的能力 | |
| C. | 电视机工作时,屏表面温度较高而吸附灰尘 | |
| D. | 电视机工作时,屏表面有静电而吸附灰尘 |
2.甲、乙两物体都做匀速圆周运动,其质量之比为1:2,转动半径之比为1:2,在相等时间里甲转过30°,乙转过45°,则它们所受外力的合力之比为( )
| A. | 1:4 | B. | 1:6 | C. | 9:16 | D. | 1:9 |
19.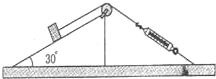 如图所示,斜面的角为30°,质量为M=2kg,有一质量m=1.0kg的物体放在斜面上用细绳相连.细绳的一端跨过摩擦不计的定滑轮与固定的轻弹簧秤相连.斜面和物体均静止在水平地面上,弹簧秤的示数为4.9N.关于物体受力的判断(取g=9.8m/s2),下列说法正确的是( )
如图所示,斜面的角为30°,质量为M=2kg,有一质量m=1.0kg的物体放在斜面上用细绳相连.细绳的一端跨过摩擦不计的定滑轮与固定的轻弹簧秤相连.斜面和物体均静止在水平地面上,弹簧秤的示数为4.9N.关于物体受力的判断(取g=9.8m/s2),下列说法正确的是( )
 如图所示,斜面的角为30°,质量为M=2kg,有一质量m=1.0kg的物体放在斜面上用细绳相连.细绳的一端跨过摩擦不计的定滑轮与固定的轻弹簧秤相连.斜面和物体均静止在水平地面上,弹簧秤的示数为4.9N.关于物体受力的判断(取g=9.8m/s2),下列说法正确的是( )
如图所示,斜面的角为30°,质量为M=2kg,有一质量m=1.0kg的物体放在斜面上用细绳相连.细绳的一端跨过摩擦不计的定滑轮与固定的轻弹簧秤相连.斜面和物体均静止在水平地面上,弹簧秤的示数为4.9N.关于物体受力的判断(取g=9.8m/s2),下列说法正确的是( )| A. | 地面对斜面体的摩擦力大小为零 | |
| B. | 斜面对物体的摩擦力大小不为零 | |
| C. | 地面 对斜面的支持力大于29.4N,方向垂直地面向上 | |
| D. | 地面对物体的支持力小于29.4N,方向垂直地面向上 |
20.做匀速圆周运动的物体,下列物理量变化的是( )
| A. | 线速度 | B. | 速率 | C. | 频率 | D. | 周期 |
16.声波在水中的速度大于在空气中的速度,让某一波源发出的声波通过空气和水中的相同的小孔,下列说法正确的是( )
| A. | 在水中的波长大于在空气中的波长,在水中更容易出现衍射现象 | |
| B. | 在水中的波长小于在空气中的波长,在水中更容易出现衍射现象 | |
| C. | 在水中的波长大于在空气中的波长,在空气中更容易出现衍射现象 | |
| D. | 在水中的波长小于在空气中的波长,在空气中更容易出现衍射现象 |
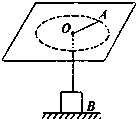 如图所示,在光滑的水平桌面上有一光滑小孔O,一根轻绳穿过小孔,一端连接质量为m=1kg的小球A,另一端连接质量为M=4kg的重物B.(g=10m/s2)试求:
如图所示,在光滑的水平桌面上有一光滑小孔O,一根轻绳穿过小孔,一端连接质量为m=1kg的小球A,另一端连接质量为M=4kg的重物B.(g=10m/s2)试求: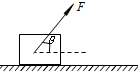 如图所示,质量为m=10kg的箱子在拉力F的作用下沿水平地面运动,拉力F=50N,方向与水平面的夹角为θ=53°,箱子与水平地面的动摩擦因数为0.20.
如图所示,质量为m=10kg的箱子在拉力F的作用下沿水平地面运动,拉力F=50N,方向与水平面的夹角为θ=53°,箱子与水平地面的动摩擦因数为0.20.