题目内容
3.如图为某生产流水线工作原理示意图.足够长的工作平台上有一小孔A,一定长度的操作板(厚度可忽略不计)静止于小孔的左侧,某时刻开始,零件(可视为质点)被无初速度地放上操作板中点,同时操作板在电动机带动下向右做匀加速直线运动直至运动到A孔的右侧(忽略小孔对操作板运动的影响),最终零件运动到A孔时速度恰好为零,并由A孔下落进入下一道工序.已知零件与操作板间的动摩擦因素μ1=0.05,与工作台间的动摩擦因素μ2=0.025,操作板与工作台间的动摩擦因素μ3=0.3.试问: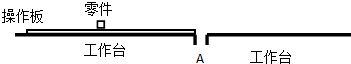
(1)电动机对操作板所施加的力是恒力还是变力(只要回答是“变力”或“恒力”即可)?
(2)操作板做匀加速直线运动的加速度a的大小为多少?
(3)若操作板长L=2m,质量M=3kg,零件的质量m=0.5kg,重力加速度取g=10m/s2,则操作板从A孔左侧完全运动到右侧过程中,电动机至少做了多少功?
分析 (1)零件离开操作板后,操作板对工作台的压力减小,故滑动摩擦力减小,故电动机对操作板所施加的力是变力;
(2)对零件在板上和工作台上分别运用牛顿第二定律列式求解加速度,然后根据运动学公式列式后联立求解;
(3)电动机做功等于消耗的电能,转化为零件动能、工作台动能,各个不为摩擦产生的内能,根据能量守恒定律和功能关系列式求解.
解答 解:(1)变力;
(2)设零件相对于工作台运动距离为x,历时为t时与操作板分离,此后零件在工作台上做匀减速运动直到A点时速度减为零.
设零件的质量为m,板长为L,取水平向右为正方向,则有:
μ1mg=ma1 ①
-μ2mg=ma2 ②
$x=\frac{1}{2}{a}_{1}{t}^{2}$ ③
从开始运动到零件与板分离,板的位移大小比零件多$\frac{L}{2}$,则有
$\frac{1}{2}a{t}^{2}=\frac{L}{2}+x$ ④
零件从开始运动到运动到A点,总位移大小为$\frac{L}{2}$,则有
x+$\frac{0-({a}_{1}t)^{2}}{2{a}_{2}}$=$\frac{L}{2}$ ⑤
联立以上各式可得:
a=$\frac{(2{μ}_{1}{μ}_{2}+{μ}_{1}^{2})g}{{μ}_{2}}$ ⑥
代入数据得:
a=2m/s2
(3)将a=2m/s2 及L=2m代入上述方程可得:
x=$\frac{1}{3}$m,t=$\frac{2}{\sqrt{3}}$s
由能量守恒可知电动机做功至少包含以下几部分:
①操作板动能的增加
$△{E}_{k1}=\frac{1}{2}M(\sqrt{2aL})^{2}$-0=12J
②零件在运动t时间内动能的增加
$△{E}_{k2}=\frac{1}{2}m({μ}_{1}gt)^{2}-0=\frac{1}{12}J$
③零件在运动t时间内与操作板摩擦而产生的内能
${E}_{3}={μ}_{1}mg•\frac{L}{2}=0.25J$
④操作板在运动t时间内与工作台摩擦而产生的内能
${E}_{4}={μ}_{3}(m+M)g(\frac{L}{2}+x)=14J$
⑤操作板从与零件分离到运动至工作台右侧过程中与工作台摩擦而产生的内能
${E}_{5}={μ}_{3}Mg(\frac{L}{2}-x)=6J$
所以电动机做功至少为
E=△Ek1+△Ek2+E3+E4+E5=32.33J
答:(1)电动机对操作板所施加的力是变力;
(2)操作板做匀加速直线运动的加速度a的大小为2m/s2;
(3)操作板从A孔左侧完全运动到右侧过程中,电动机至少做32.33J的功.
点评 该题中,对零件的运动过程的分析是解题的关键.要紧扣题目给出的条件:最终零件运动到A孔时速度恰好为零!得出零件的正确的运动过程.

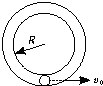 如图所示,一半径为R的光滑圆形细管,固定于竖直平面内,放置于管内最低处的小球以初速度v0沿管内运动,欲使小球能通过管的最高点,且小球在最高点时对管壁有向下的压力,v0必须满足的条件是( )
如图所示,一半径为R的光滑圆形细管,固定于竖直平面内,放置于管内最低处的小球以初速度v0沿管内运动,欲使小球能通过管的最高点,且小球在最高点时对管壁有向下的压力,v0必须满足的条件是( )| A. | v0≤2$\sqrt{Rg}$ | B. | v0≥$\sqrt{5Rg}$ | C. | v0≤2$\sqrt{Rg}$或v0≥$\sqrt{5Rg}$ | D. | 2$\sqrt{Rg}$≤v0≤$\sqrt{5Rg}$ |
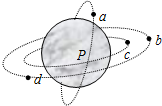 如图所示,a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d在同一个圆轨道上.某时刻b卫星恰好处于c卫星的正上方.下列说法中正确的是( )
如图所示,a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星.其中a、c的轨道相交于P,b、d在同一个圆轨道上.某时刻b卫星恰好处于c卫星的正上方.下列说法中正确的是( )| A. | a、c的线速度大小相等,且小于d的线速度 | |
| B. | b、c的角速度大小相等,且小于a的角速度 | |
| C. | a、c的加速度大小相等,且大于b的加速度 | |
| D. | b、d存在相撞危险 |
| A. | 磁场对电流产生力的作用 | |
| B. | 变化的磁场使闭合电路产生感应电流 | |
| C. | 插入通电螺线管中的软铁棒被磁化 | |
| D. | 电流周围产生磁场 |
| A. | 提高输送功率 | B. | 提高输电的电流 | ||
| C. | 提高高压输电的电压 | D. | 减小输电导线的横截面积 |
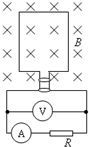 如图所示,交流发电机的矩形线框长为0.4m,宽为0.2m,共有50匝线圈,其电阻r=1.0Ω,在磁感应强度B=0.2T的匀强磁场中,绕垂直于磁场方向的对称轴OO′,以$\frac{100}{π}$r/s的转速匀速转动,向R=9.0Ω的电阻供电.从线框处于中性面开始计时,求
如图所示,交流发电机的矩形线框长为0.4m,宽为0.2m,共有50匝线圈,其电阻r=1.0Ω,在磁感应强度B=0.2T的匀强磁场中,绕垂直于磁场方向的对称轴OO′,以$\frac{100}{π}$r/s的转速匀速转动,向R=9.0Ω的电阻供电.从线框处于中性面开始计时,求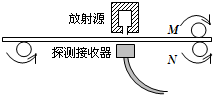 如图是利用放射线自动控制铝板厚度的装置.假如放射源能放射出α、β、γ三种射线,而根据设计,该生产线压制的是3mm厚的铝板,那么是三种射线中的β射线对控制厚度起主要作用.当探测接收器单位时间内接收到的放射性粒子的个数超过标准值时,将会通过自动装置将M、N两个轧辊间的距离调节得远些(“远”或“近”).
如图是利用放射线自动控制铝板厚度的装置.假如放射源能放射出α、β、γ三种射线,而根据设计,该生产线压制的是3mm厚的铝板,那么是三种射线中的β射线对控制厚度起主要作用.当探测接收器单位时间内接收到的放射性粒子的个数超过标准值时,将会通过自动装置将M、N两个轧辊间的距离调节得远些(“远”或“近”).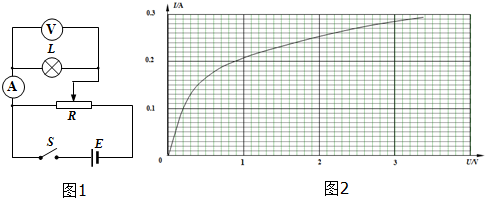
 如图所示,甲、乙两船相距40m,一列水波在水面上从左向右传播,某时刻波形如图所示,甲船位于波峰时乙船恰位于波谷,且峰、谷间的高度差为0.4m.若波速为4m/s,试求:
如图所示,甲、乙两船相距40m,一列水波在水面上从左向右传播,某时刻波形如图所示,甲船位于波峰时乙船恰位于波谷,且峰、谷间的高度差为0.4m.若波速为4m/s,试求: