题目内容
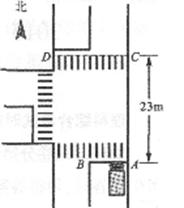
(12分)A、B两物体(视为质点)在同一直线上同时出发向同一方向运动,物体A从静止开始做匀加速直线运动,加速度的大小a=2m/s2,物体B在A的后面相距L=16m处,以v1=10m/s的速度做匀速运动。两物体追逐时,互从近旁通过,不会相碰。求:
(1)经过多长时间物体B追上物体A?
(2)共经过多长时间A、B两物体再次相遇?
(3)A、B两物体两次相遇之间相距最远的距离是多少?
(1)t1="8s" (2)t2="8s" (3)s=9m
解析试题分析: (1)设经过t1,B物体追上A物体则有: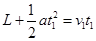 (2分)
(2分)
解得t1=2s(2分)
(2)设共经过t2,A物体追上B物体,由上面方程可得t2=8s(1分)
(3)设A、B两物体再次相遇前两物体相距最远距离为s,所用时间为t,此时A、B物体有相同的速度v1,
v1=at(1分) (2分)
(2分)
联立可得:s=9m(2分)
考点:本题考查了匀变速直线运动的追及和相遇问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图所示,AB为粗糙程度不变的水平地面,BC为粗糙程度不变的斜面,B点有微小的圆弧与两个面相切过渡。一物体(可看作质点)从A点以某一速度出发做匀减速运动并冲上斜面BC直到速度为零,以出发点为计时起点,各时间点的速度如下表所述。试求物体在斜面上运动的最远距离。
| t(s) | 0 | 1 | 2 | 3 | 4 | 5 |
| V(m/s) | 15 | 13 | 11 | 8 | 4 | 0 |
如图所示,斜面倾角为 ,斜面上AB段光滑,其它部分粗糙,且斜面足够长。一带有速度传感器的小物块(可视为质点),自A点由静止开始沿斜面下滑,速度传感器上显示的速度v与运动时间t的关系如下表所示:
,斜面上AB段光滑,其它部分粗糙,且斜面足够长。一带有速度传感器的小物块(可视为质点),自A点由静止开始沿斜面下滑,速度传感器上显示的速度v与运动时间t的关系如下表所示:
| 时间t/s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 速度v/ms-1 | 0 | 6 | 12 | 17 | 21 | 25 | 29 | |
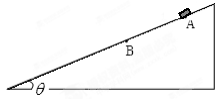
(1)斜面的倾角
 多大?
多大?(2)小物块与斜面的粗糙部分间的动摩擦因数μ为多少?
(3)AB间的距离
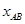 等于多少?
等于多少? 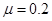 。从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F的作用,力F 随时间的变化规律如图9所示。重力加速度
。从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F的作用,力F 随时间的变化规律如图9所示。重力加速度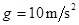 , 求:
, 求:
 的大小和方向;
的大小和方向; 时物块运动的瞬时速度
时物块运动的瞬时速度 的大小和方向;
的大小和方向;