题目内容
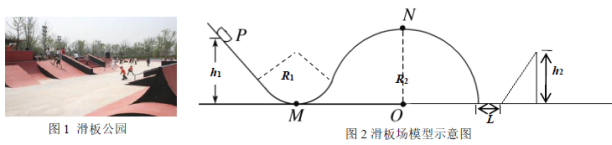
【题目】滑板项目是极限运动历史的鼻祖，在滑板公园里经常看到各种滑板场地，如图1所示。现有一个滑板场可简化为如下模型，如图2所示，由足够长的斜直轨道、半径
m的凹形圆弧轨道和半径
m的凸形圆弧轨道三部分组成的滑板组合轨道。 这三部分轨道依次平滑连接，且处于同一竖直平面内。 其中M点为凹形圆弧轨道的最低点，N点为凸形圆弧轨道的最高点，凸形圆弧轨道的圆心O与M点在同一水平面上。一可视为质点、质量为m=1kg的滑板从斜直轨道上的P点无初速度滑下，经M点滑向N点。在凸形圆弧最右侧距离L=0. 9m的位置有一个高度
m、倾角为53°的斜面。不计一切阻力，g取10m/s2. 求：
(1)若P点距水平面的高度
m，滑板滑至M点时，轨道对滑板的支持力大小FN；
(2)若滑板滑至N点时对轨道恰好无压力，求滑板的下滑点P距水平面的高度H；
(3)若滑板滑至N点时刚好做平抛运动，滑板能否与右侧斜面发生碰撞（不考虑碰撞后反弹）？若能，请计算出碰撞的具体位置；若不能，请说明理由。
【答案】（1）42N；（2）5.4m；（3）能，见解析
【解析】
（1）滑板由P点滑至M点过程，由机械能守恒有
得
vM=8m/s.
对滑板滑至M点时受力分析，由牛顿第二定律有
得
FN=42N.
（2）滑板滑至N点时对轨道恰好无压力，则有
得
vN=6m/s
滑板从P点到N点机械能守恒，则有
解得
H=5.4m.
（3）由平抛运动的规律
x=vNt
解得
t=0.8s
则碰撞点距离斜面底端的水平距离为0.3m，距离斜面底端的高度为0.4m。
练习册系列答案
相关题目
