题目内容
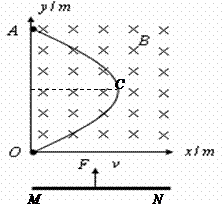
如图所示,在坐标 xoy 平面内存在 B =2.0T的匀强磁场,OA 与OCA 为置于竖直平面内的光滑金属导轨,其中OCA 满足曲线方程![]() ,C为导轨的最右端,导轨OA 与OCA 相交处的O点和A 点分别接有体积可忽略的定值电阻R1 和 R2,其R1 = 4.0Ω、R2 = 12.0Ω。现有一足够长、质量 m = 0.10 kg 的金属棒 M N 在竖直向上的外力F 作用下,以v =3.0m/s的速度向上匀速运动,设棒与两导轨接触良好,除电阻 R1、R2 外其余电阻不计,g 取10m/s2,求:
,C为导轨的最右端,导轨OA 与OCA 相交处的O点和A 点分别接有体积可忽略的定值电阻R1 和 R2,其R1 = 4.0Ω、R2 = 12.0Ω。现有一足够长、质量 m = 0.10 kg 的金属棒 M N 在竖直向上的外力F 作用下,以v =3.0m/s的速度向上匀速运动,设棒与两导轨接触良好,除电阻 R1、R2 外其余电阻不计,g 取10m/s2,求:
(1)金属棒 M N 在导轨上运动时感应电流的最大值;
(2)外力F 的最大值;
(3)金属棒 M N 滑过导轨O C 段,整个回路产生的热量。
(1) ![]() A
A
(2) ![]() N
N
(3) ![]() J.
J.
解析:
(1)金属棒MN沿导轨竖直向上运动,进入磁场中切割磁感线产生感应电动势。当金属棒MN匀速运动到C点时,电路中感应电动势最大,产生的感应电流最大。
金属棒MN接入电路的有效长度为导轨OCA形状满足的曲线方程中的x值。因此接入电路的金属棒的有效长度为
![]() Lm=xm=0.5m
Lm=xm=0.5m
![]() Em=3.0V
Em=3.0V
![]() 且
且![]()
![]() A
A
(2)金属棒MN匀速运动中受重力mg、安培力F安、外力F外作用
![]()
![]() N
N
![]()
![]() N
N
(3)金属棒MN在运动过程中,产生的感应电动势
![]() 有效值为
有效值为 ![]()
金属棒MN滑过导轨OC段的时间为t
![]()
![]() m
m
![]() s
s
滑过OC段产生的热量 ![]()
![]() J.
J.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1)下列说法正确的是
(1)下列说法正确的是 磁聚焦被广泛的应用在电真空器件中,如图所示,在坐标xoy中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为
磁聚焦被广泛的应用在电真空器件中,如图所示,在坐标xoy中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为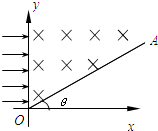 (2005?衡阳模拟)如图所示,在坐标的第Ⅰ象限内有一匀强磁场区域,磁感应强度为B,y轴是磁场左侧的边界,直线OA是磁场右侧的边界,在第Ⅱ象限y>0的区域,有一束带电量为q的负粒子(重力不计)垂直y轴射入磁场,粒子的质量为m,粒子在各入射点速度与入射点的y轴坐标值成正比,即v=by(b是常数,且b>0).要求粒子穿过磁场区域后,都垂直于x轴射出,求:直线OA与x轴的夹角θ多大?(用题中已知物理量符号表示)
(2005?衡阳模拟)如图所示,在坐标的第Ⅰ象限内有一匀强磁场区域,磁感应强度为B,y轴是磁场左侧的边界,直线OA是磁场右侧的边界,在第Ⅱ象限y>0的区域,有一束带电量为q的负粒子(重力不计)垂直y轴射入磁场,粒子的质量为m,粒子在各入射点速度与入射点的y轴坐标值成正比,即v=by(b是常数,且b>0).要求粒子穿过磁场区域后,都垂直于x轴射出,求:直线OA与x轴的夹角θ多大?(用题中已知物理量符号表示) 如图所示,在坐标原点O处,能向四周均匀发射速度大小相等、方向都平行于纸面的带正电粒子.在O点右侧有一半径为R的圆形薄板,薄板中心O′位于x轴上,且与x轴垂直放置,薄板的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速率为v,重力不计.
如图所示,在坐标原点O处,能向四周均匀发射速度大小相等、方向都平行于纸面的带正电粒子.在O点右侧有一半径为R的圆形薄板,薄板中心O′位于x轴上,且与x轴垂直放置,薄板的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速率为v,重力不计.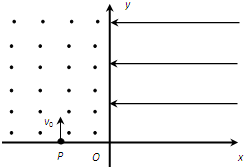 如图所示,在坐标平面的第Ⅰ象限内有水平向左的匀强电场E=1.0×103V/m,第Ⅱ象限内有垂直纸面向外的匀强磁场B=0.4T,一荷质比为
如图所示,在坐标平面的第Ⅰ象限内有水平向左的匀强电场E=1.0×103V/m,第Ⅱ象限内有垂直纸面向外的匀强磁场B=0.4T,一荷质比为