题目内容
20. 如图所示,空间有磁感应强度B=0.6T的匀强磁场,坐标原点处有一α粒子(带正电)源,在纸面内以相同大小的速度沿不同方向向第四象限发射α粒子,在x坐标轴上方16cm处有一足够大的与x轴平行与y轴垂直的挡板,己知α粒子的比荷$\frac{q}{m}=5×{10^7}$C/kg,速度为3×106m/s,则可以打到挡板的α粒子从原点射出时其速度方向与x轴正向最大夹角为( )
如图所示,空间有磁感应强度B=0.6T的匀强磁场,坐标原点处有一α粒子(带正电)源,在纸面内以相同大小的速度沿不同方向向第四象限发射α粒子,在x坐标轴上方16cm处有一足够大的与x轴平行与y轴垂直的挡板,己知α粒子的比荷$\frac{q}{m}=5×{10^7}$C/kg,速度为3×106m/s,则可以打到挡板的α粒子从原点射出时其速度方向与x轴正向最大夹角为( )| A. | 30° | B. | 37° | C. | 53° | D. | 60° |
分析 根据带电粒子在匀强磁场中运动的半径公式求出带电粒子运动的半径,抓住半径不变,作动态圆,当带电粒子初速度方向沿x轴正方向时,打到挡板的α粒子的速度方向与x轴正向的夹角最大.
解答 解: 带电粒子在匀强磁场中运动的轨道半径为:
带电粒子在匀强磁场中运动的轨道半径为:
r=$\frac{mv}{qB}=0.1m=10cm$.
当带电粒子的初速度方向沿x轴正向时,打到挡板的α粒子其速度方向与x轴正向的夹角最大.有:sin$α=\frac{\sqrt{1{0}^{2}-{6}^{2}}}{10}=0.8$,
则最大角为:α=53°.故C正确,A、B、D错误.
故选:C.
点评 本题对数学要求的能力要求较高,抓住圆周运动的半径为定值,通过动态圆来确定打到挡板的α粒子的速度方向与x轴正向的夹角何时最大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.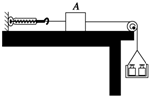 如图所示,放在水平桌面上的木块A处于静止状态,所挂的托盘和砝码总质量为0.6kg,弹簧秤读数为2N,滑轮摩擦不计.若轻轻取走部分砝码,使总质量减
如图所示,放在水平桌面上的木块A处于静止状态,所挂的托盘和砝码总质量为0.6kg,弹簧秤读数为2N,滑轮摩擦不计.若轻轻取走部分砝码,使总质量减
小为0.4kg,将会出现的情况是(g=10m/s2)( )
 如图所示,放在水平桌面上的木块A处于静止状态,所挂的托盘和砝码总质量为0.6kg,弹簧秤读数为2N,滑轮摩擦不计.若轻轻取走部分砝码,使总质量减
如图所示,放在水平桌面上的木块A处于静止状态,所挂的托盘和砝码总质量为0.6kg,弹簧秤读数为2N,滑轮摩擦不计.若轻轻取走部分砝码,使总质量减小为0.4kg,将会出现的情况是(g=10m/s2)( )
| A. | 物体A将具有向左运动的趋势 | B. | 弹簧秤的读数减小 | ||
| C. | 物体A将向左运动 | D. | 物体受到的摩擦力为2N |
8.“神舟”九号飞船上的电子仪器及各种动作的控制都是靠太阳能电池供电的.由于光照而产生电动势的现象称为光伏效应.“神舟”九号飞船上的太阳能电池就是依靠光伏效应设计的单晶硅太阳能电池.在正常照射下,太阳能电池的光电转换效率可达23%.单片单晶硅太阳能电池可产生0.6V的电动势,可获得0.1A的电流,则每秒照射到这种太阳能电池上的太阳光的能量是( )
| A. | 0.24 J | B. | 0.25 J | C. | 0.26 J | D. | 0.28 J |
15. 如图所示,两块不带电的竖直平行金属板相距为d,一个重为G的带电小球在重力作用下在两板间竖直下落,此时小球的运动轨迹是AB,当两板间加上电压U时,小球受力方向变成沿BC方向,则此小球所带的电荷量应是( )
如图所示,两块不带电的竖直平行金属板相距为d,一个重为G的带电小球在重力作用下在两板间竖直下落,此时小球的运动轨迹是AB,当两板间加上电压U时,小球受力方向变成沿BC方向,则此小球所带的电荷量应是( )
 如图所示,两块不带电的竖直平行金属板相距为d,一个重为G的带电小球在重力作用下在两板间竖直下落,此时小球的运动轨迹是AB,当两板间加上电压U时,小球受力方向变成沿BC方向,则此小球所带的电荷量应是( )
如图所示,两块不带电的竖直平行金属板相距为d,一个重为G的带电小球在重力作用下在两板间竖直下落,此时小球的运动轨迹是AB,当两板间加上电压U时,小球受力方向变成沿BC方向,则此小球所带的电荷量应是( )| A. | $\frac{G}{U}$ | B. | $\frac{G}{2U}$ | C. | $\frac{Gd}{U}$ | D. | $\frac{2Gd}{U}$ |
12. 如右图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )
如右图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )
 如右图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )
如右图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )| A. | b所需向心力最大 | |
| B. | b、c周期相等,且大于a的周期 | |
| C. | b、c向心加速度相等,且大于a的向心加速度 | |
| D. | b、c的线速度大小相等,且小于a的线速度 |
9. 将一电荷量为Q的小球甲放在一个事先不带电的金属球乙附近,所形成的电场线分布如图所示,金属球乙表面的电势处处相等.a、b为电场中的两点,根据图中信息,可判断( )
将一电荷量为Q的小球甲放在一个事先不带电的金属球乙附近,所形成的电场线分布如图所示,金属球乙表面的电势处处相等.a、b为电场中的两点,根据图中信息,可判断( )
 将一电荷量为Q的小球甲放在一个事先不带电的金属球乙附近,所形成的电场线分布如图所示,金属球乙表面的电势处处相等.a、b为电场中的两点,根据图中信息,可判断( )
将一电荷量为Q的小球甲放在一个事先不带电的金属球乙附近,所形成的电场线分布如图所示,金属球乙表面的电势处处相等.a、b为电场中的两点,根据图中信息,可判断( )| A. | 甲球带正电,乙球带电量为Q的负电 | |
| B. | 检验电荷-q在a点的电势能比在b点的大 | |
| C. | a点的场强比b点的大,同时a点的电势也比b点的高 | |
| D. | 将检验电荷-q从a点移到b点的过程中,电场力做正功 |
 如图所示,四分之一圆轨道OA与水平轨道AB相切,它们与另一水平轨道CD在同一竖直面内,圆轨道OA的半径R=0.45m,水平轨道AB长s1=3m,OA与AB均光滑.一滑块从O点由静止释放,当滑块经过A点时,静止在CD上的小车在F=1.6N的水平恒力作用下启动,运动一段时间后撤去力F.当小车在CD上运动了s2=3.28m时速度v=2.4m/s,此时滑块恰好落入小车中.已知小车质量M=0.2kg,与CD间的动摩擦因数μ=0.4,取g=10m/s2,求:
如图所示,四分之一圆轨道OA与水平轨道AB相切,它们与另一水平轨道CD在同一竖直面内,圆轨道OA的半径R=0.45m,水平轨道AB长s1=3m,OA与AB均光滑.一滑块从O点由静止释放,当滑块经过A点时,静止在CD上的小车在F=1.6N的水平恒力作用下启动,运动一段时间后撤去力F.当小车在CD上运动了s2=3.28m时速度v=2.4m/s,此时滑块恰好落入小车中.已知小车质量M=0.2kg,与CD间的动摩擦因数μ=0.4,取g=10m/s2,求: