题目内容
 如图所示,同一竖直平面内固定着两水平绝缘细杆AB.CD,长均为L,两杆间竖直距离为h,BD两端以光滑绝缘的半圆形细杆相连,半圆形细杆与AB.CD在同一竖直面内,且AB.CD恰为半圆形圆弧在B.D两处的切线,O为AD.BC连线的交点,在O点固定一电量为Q的正点电荷.质量为m的小球P带正电荷,电量为q,穿在细杆上,从A以一定初速度出发,沿杆滑动,最后可到达C点.已知小球与两水平杆之间动摩擦因数为μ,小球所受库仑力始终小于小球重力.则( )
如图所示,同一竖直平面内固定着两水平绝缘细杆AB.CD,长均为L,两杆间竖直距离为h,BD两端以光滑绝缘的半圆形细杆相连,半圆形细杆与AB.CD在同一竖直面内,且AB.CD恰为半圆形圆弧在B.D两处的切线,O为AD.BC连线的交点,在O点固定一电量为Q的正点电荷.质量为m的小球P带正电荷,电量为q,穿在细杆上,从A以一定初速度出发,沿杆滑动,最后可到达C点.已知小球与两水平杆之间动摩擦因数为μ,小球所受库仑力始终小于小球重力.则( )分析:小球与正电荷之间的库仑力是排斥力,当小球在O点正下方时小球受到向下的库仑力最大,此时正压力最大,摩擦力最大,同理当小球在O点正上方时摩擦力最小;可以利用微元法并结合对称性及求出小球在AB和CD杆上运动时摩擦力做的功.
解答:解:A、B、小球在O点正下方时受到向下的库仑力最大,此时正压力最大,摩擦力最大,故:
fmax=μNmax=μ[mg+
]=μ(mg+
);故A错误,B正确;
C、D、利用微元法并结合对称性:在AB和CD杆上运动△s位移时,摩擦力做的功为:△W=μ(mg+Fy)△s+μ(mg-Fy)△s=2μmg△s,所以从A到C过程中摩擦力做的功为W=△W1+△W2+…=2μmgl,故C错误,D错误;
故选:B.
fmax=μNmax=μ[mg+
| kQq | ||
(
|
| 4kQq |
| h2 |
C、D、利用微元法并结合对称性:在AB和CD杆上运动△s位移时,摩擦力做的功为:△W=μ(mg+Fy)△s+μ(mg-Fy)△s=2μmg△s,所以从A到C过程中摩擦力做的功为W=△W1+△W2+…=2μmgl,故C错误,D错误;
故选:B.
点评:本题主要考查了动能定理、库仑定律、滑动摩擦力公式的直接应用,解题是要注意库伦力具有对称性,较难.

练习册系列答案
相关题目
 (2008?广州二模)如图所示,在竖直平面内有水平向右的匀强电场,同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球,另一端固定于0点,已知带电小球受到的电场力大于重力,小球由静止释放,到达图中竖直虚线前小球做( )
(2008?广州二模)如图所示,在竖直平面内有水平向右的匀强电场,同一竖直平面内水平拉直的绝缘细线一端系一带正电的小球,另一端固定于0点,已知带电小球受到的电场力大于重力,小球由静止释放,到达图中竖直虚线前小球做( )
 静止在光滑斜面底部的压缩弹簧的顶端此时小球距斜面顶端的高度为
静止在光滑斜面底部的压缩弹簧的顶端此时小球距斜面顶端的高度为 .解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时
.解除弹簧的锁定后,小球沿斜面向上运动.离开斜面后,达到最高点时(此时 发生弹性碰撞,碰撞后球
发生弹性碰撞,碰撞后球 同一高度,球
同一高度,球 上的
上的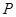 点,
点,  与
与 .已知球
.已知球 ,悬绳长
,悬绳长 ,视两球为质点,重力加速度为
,视两球为质点,重力加速度为 ,不计空气阻力.求:
,不计空气阻力.求:

