题目内容
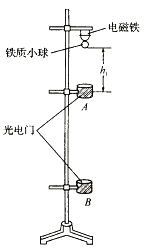
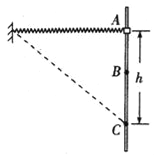
【题目】如图所示，轻弹簧的下端系着A、B两球，mA=100g，mB=500g，系统静止时弹簧伸长x=15cm，未超出弹性限度．若剪断A、B间的细绳，则A在竖直方向做简谐运动，求：
（1）A的振幅多大？
（2）A球的最大加速度多大？（g取10m/s2）
【答案】（1）12.5cm；
（2）50m/s2
【解析】试题分析：先研究AB两球，由平衡关系要得出劲度系数；刚剪断细线时小球的加速度最大，此处相当于是小球到达简谐运动的振幅处．
解：（1）只挂A球时弹簧伸长量由F=kx
得x1=
挂A、B两物体时有：kx=（mA+mB）g；
k=
=40N/m
剪断A、B间细线后，A球静止悬挂时的弹簧的伸长量为xA==0.025m
弹簧下端的这个位置就是A球振动中的平衡位置．
悬挂B球后又剪断细线，相当于用手把A球下拉后又突然释放，刚剪断细线时弹簧比静止悬挂A球多伸长的长度就是振幅，
即A=x﹣xA=15cm﹣2.5cm=12.5cm
（2）振动中A球的最大加速度为最大加速度为：
amax=
=
×10m/s2=50m/s2
答：（1）最大振幅为12.5cm；
（2）最大加速度为50m/s2．
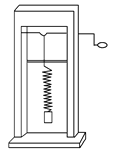
阅读快车系列答案
【题目】一砝码和一轻弹簧构成弹簧振子，图所示的装置可用于研究该弹簧振子的受迫振动．匀速转动把手时，曲轴给弹簧振子以驱动力，使振子做受迫振动．把手匀速转动的周期就是驱动力的周期，改变把手匀速转动的速度就可以改变驱动力的周期．若保持把手不动，给砝码一向下的初速度，砝码便做简谐运动，振动图像如图甲所示．当把手以某一速度匀速转动，受迫振动达到稳定时，砝码的振动图像如图乙所示．若用T0表示弹簧振子的固有周期，T表示驱动力的周期，Y表示受迫振动达到稳定后振子的振幅，则( )．
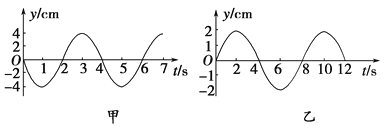
A．由图像可知T0＝4 s |
B．由图像可知T0＝8 s |
C．当T在4 s附近时，Y显著增大；当T比4 s小得多或大得多时，Y很小 |
D．当T在8 s附近时，Y显著增大；当T比8 s小得多或大得多时，Y很小 |
