题目内容
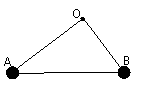
如图所示，OAB是一刚性轻质直角三角形支架，边长AB=0.2m，∠OAB=37°；在A、B两顶角处各固定一个大小不计的小球，质量均为1kg。支架可绕过O的水平轴在竖直平面内无摩擦地转动。（sin37°=0.6，cos37°=0.8，重力加速度g取10m/s2）
（1）为使支架静止时AB边水平，求在支架上施加的最小力；
（2）若将支架从AB位于水平位置开始由静止释放，求支架转动过程中A处小球速度的最大值。
（1）为使支架静止时AB边水平，求在支架上施加的最小力；
（2）若将支架从AB位于水平位置开始由静止释放，求支架转动过程中A处小球速度的最大值。
解：（1）施加的最小力满足的条件是：力臂最大
所以该力的作用在A点，方向垂直于OA向上
mg·OA·cos37°= mg·OB·cos53°+Fmin·OA
OA=0.16m，OB=0.12m，可解得Fmin=3.5N
作用在A点，在支架平面内垂直于OA向上
（2）支架力矩平衡时两小球的速度最大
设平衡时OA边与竖直方向夹角为θ
则有mg·OA·sinθ=mg·OB·sin（90°-θ），可得θ=37°
mg（OAcos37°-OAcos53°）-mg（OBcos37°-OBcos53°）=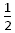
m（v12+ v22）
v1:v2= OA:OB=4:3
由上述两式可解得v1=0.32m/s
所以该力的作用在A点，方向垂直于OA向上
mg·OA·cos37°= mg·OB·cos53°+Fmin·OA
OA=0.16m，OB=0.12m，可解得Fmin=3.5N
作用在A点，在支架平面内垂直于OA向上
（2）支架力矩平衡时两小球的速度最大
设平衡时OA边与竖直方向夹角为θ
则有mg·OA·sinθ=mg·OB·sin（90°-θ），可得θ=37°
mg（OAcos37°-OAcos53°）-mg（OBcos37°-OBcos53°）=
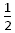m（v12+ v22）v1:v2= OA:OB=4:3
由上述两式可解得v1=0.32m/s
练习册系列答案
相关题目
如图所示，OAB是一刚性轻质直角三角形支架，边长AB=0.2m，∠OAB=37°；在A、B两顶角处各固定一个大小不计的小球，质量均为1kg．支架可绕过O的水平轴在竖直平面内无摩擦地转动．（sin37°=0.6，cos37°=0.8，重力加速度g取10m/s2）
