��Ŀ����
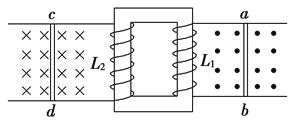
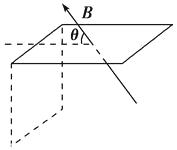
����Ŀ����ͼ�����̶��ľ�Եб����Ǿ�Ϊ�ȣ�������������ϸ������ab�������a�ˣ���cd�������c�ˣ����Ⱦ�ΪL�������ֱ�Ϊ2m��m�������������쳤���������߽��������ɱպϻ�·abdca����ͨ���̶���б�����ص����⻬��ԵС�����ֿ����б���ϣ�ʹ��������ˮƽ����б���ϴ�����ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB������ֱ��б�����ϣ���֪�������߸պò��ڴų��У���·����ΪR������������б���Ķ�Ħ��������Ϊ�̣��������ٶȴ�СΪg����֪������ab�����»�����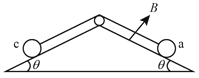
�������ڽ�����ab�ϵİ������Ĵ�С��
�ڽ������˶��ٶȵĴ�С��
���𰸡��⣺���赼�ߵ������Ĵ�СΪT����б���ab����֧�����Ĵ�СΪ ![]() ��������ab���ϵİ������Ĵ�СΪF����б���cd��֧������СΪ
��������ab���ϵİ������Ĵ�СΪF����б���cd��֧������СΪ ![]() ������ab����������ƽ��������
������ab����������ƽ��������![]() ��
��![]() ��
��
����cd����ͬ����![]() ��
��![]() ��
��
�����٢ڢۢ�ʽ��
F=mg��sin�ȩ�3��cos�ȣ���
���ɰ�������ʽ��
F=BIL��
����I��abcda�еĸ�Ӧ������ab���ϵĸ�Ӧ�綯��Ϊ
=BLv��
ʽ�У�v��ab���»��ٶȵĴ�С����ŷķ���ɵ�![]() ��
��
�����ݢޢߢ�ʽ��![]() ��
��
�𣺢������ڽ�����ab�ϵİ������Ĵ�Сmg��sin�ȩ�3��cos�ȣ����ڽ������˶��ٶȵĴ�С ![]() ��
��
���������ٶ�ab��cd�����ݹ�����ƽ����ʽ�������ڽ�����ab�ϵİ������Ĵ�С�ڸ��ݰ�������ʽ����Ӧ�綯�ƺͱպϵ�·ŷķ����������⣻�����ǵ�Ÿ�Ӧ�е���ѧƽ�����⣬�漰�����ڵ�Ÿ�Ӧ���ɺͱպϵ�·��ŷķ���ɵ�֪ʶ�㣬���������ͼ��㰲�����ǹؼ���

 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�