题目内容
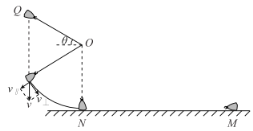
【题目】某建筑工人从高处向楼下运送细沙时，想出了一个巧妙的办法，如图所示，在树杈上的O点系一长度为R的轻质细绳，绳子另一端系铁钩(重力和大小忽略不计)，在阳台上Q点拉直绳子并将铁钩勾住沙袋，OQ与水平方向的夹角为
=30°，将沙袋由静止释放，沙袋运动到O点正下方N点时正好脱钩(脱钩过程中，沙袋无能量损失)，沿水平地面滑到M点停下。已知沙袋可视为质点，质量为m，O、N两点之间的距离为R，M、N两点之间的距离为2R，重力加速度为g，空气阻力不计，求：
（1）沙袋运动到N点时的速度大小；
（2）沙袋运动到N点脱钩前瞬间绳子的张力大小及沙袋与地面间的动摩擦因数。
【答案】（1）
；（2）
；0.625
【解析】
（1）沙袋由静止释放后先竖直下落，绳子张紧后做圆周运动，如图所示
沙袋竖直下落过程中，由机械能守恒定律有
解得
绳子张紧后，沿半径方向的速度消失，沿圆弧切线方向的速度
此后沙袋做圆周运动，从绳子张紧位置运动至N点过程，由机械能守恒定律有
解得
（2）沙袋运动到N点脱钩前，根据牛顿运动定律有
可得绳子的张力
由能量守恒定律有
解得
μ=0.625
练习册系列答案
相关题目
