题目内容
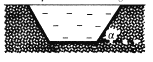
【题目】如图所示为某水池的截面图，其截面为深度h=2m、上底宽度d=4m的等腰梯形，当水池加满水且阳光与水平面的夹角θ最小时（为37°），阳光恰好可以照射到整个水池的底部。已知水池的腰与水平面的倾角
=53° ，sin 53°=0.8，cos 53°=0.6.
（i）求水池中水的折射率；
（ii）若在水池底部中心放一点光源，求站在池边的观察者看到光源的最小视深H。（结果可带根号）
【答案】（ⅰ）
；（ⅱ）
。
【解析】
(ⅰ)水池加满水时，阳光可以照射到整个水池的底部，则水池的腰与水平面的倾角
要等于折射光与地面的夹角，折射角
设入射角为
，有
由折射定理有
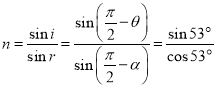
解得
(ⅱ)因为
当点光源发出的光线从池边缘射出时，设入射角为，则由几何关系可知
，故此时观察者可以看到光源且视深最小；
设此时光线的出射角为
，则由折射定律有
由几何关系可知
解得
练习册系列答案
相关题目
