题目内容

【题目】一根长为l的细绳，一端系一小球，另一端悬挂于O点．将小球拉起使细绳与竖直方向成600角，如图所示，在O点正下方有A、B、C三点，并且有．当在A处钉钉子时，小球由静止下摆，被钉子挡住后继续摆动的最大高度为hA；当在B处钉钉子时，小球由静止下摆，被钉子档住后继续摆动的最大高度为hB；当在C处钉钉子时，小球由静止下摆，被钉子挡住后继续摆动的最大高度为hC，则小球摆动的最大高度hA、hB、hC（与D点的高度差）之间的关系是（ ）

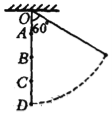
A．hA = hB = hC B．hA >hB > hC

C．hA > hB = hC D．hA = hB > hC

【答案】D

【解析】

试题分析：由于，因此碰到A、B处的钉子时，小球继续摆动，到达最高点时没能超过A、B点的位置，因此速度为零，根据机械能守恒定律，摆动的最高点与初始位置等高，而碰到C处的钉子向左摆动，当高度超过C点高度而又不能做一个完整的圆周运动，因此会脱离圆周做抛做运动，到达最高点时速度不为零，根据机械能守恒，高度小于碰到A、B处的钉子的高度，因此D正确，ABC错误，

练习册系列答案
相关题目

【题目】下列说法正确的是_________

A.全息照片的拍摄利用了光的衍射原理

B.只有发生共振时，受迫振动的频率才等于驭动力的频率

C.以接近光速运动的物体，其质量比静止时的大

D.变化的电场一定产生磁场，均匀变化的电场产生的磁场是稳定的

E.鸣笛汽车驶近路人的过程中，路人听到的声波报率与该波源的预率相比增大了

【题目】为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(碰撞过程中没有机械能损失)，某同学选取了两个体积相同、质量不等的小球，按下述步骤做如下实验：

①用天平测出两个小球的质量分别为m1和m2，且m1>m2；

②按照如图所示的那样，安装好实验装置。将斜槽AB固定在桌边，使槽的末端点的切线水平，将一斜面BC连接在斜槽末端；

③先不放小球m2，让小球m1从斜槽顶端A处由静止开始滚下，记下小球在斜面上的落点位置；

④将小球m2放在斜槽前端边缘处，让小球m1仍从斜槽顶端A处静止开始滚下，使它们发生碰撞，记下小球m1和小球m2在斜面上的落点位置；

⑤用毫米刻度尺量出各个落点位置到斜槽末端点B的距离。图中D、E、F点是该同学记下的小球在斜面上的几个落点位置，到B点的距离分别为LD、LE、LF

根据该同学的实验，回答下列问题：

(1)在没有放m2时，让小球m1从斜槽顶端A处由静止开始滚下，m1的落点是图中的____________点；

(2)用测得的物理量来表示，只要满足关系式_________，则说明碰撞中动量是守恒的；

(3)用测得的物理量来表示，只要再满足关系式________________，则说明两小球的碰撞是弹性碰撞。

【题目】下列物理量中，属于矢量的是：（ ）

A. 路程 B. 质量 C. 速度 D. 时间

【题目】如图所示，内壁光滑的圆锥筒的轴线垂直于水平面，圆锥筒固定不动，两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动，则

A. 球A的角速度一定小于球B的角速度

B. 球A的线速度一定小于球B的线速度

C. 球A的运动周期一定小于球B的运动周期

D. 球A对筒壁的压力一定大于球B对筒壁的压力

【题目】如图所示，一轻质弹簧竖直固定在地面上，自然长度l0=0.50m，上面连接一个质量m1=1.0kg的物体A，平衡时物体距地面h1=0.40m，此时弹簧的弹性势能EP=0.50J。在距物体A正上方高为h=0.45m处有一个质量m2=1.0kg的物体B自由下落后，与弹簧上面的物体A碰撞并立即以相同的速度运动，已知两物体不粘连，且可视为质点。g=10m/s2。求：

（1）碰撞结束瞬间两物体的速度大小；

（2）两物体一起运动第一次具有竖直向上最大速度时弹簧的长度；

（3）两物体第一次分离时物体B的速度大小。

【题目】理想变压器原线圈a匝数n1=500，副线圈b匝数n2=100，线圈a接在如图所示的交变电压的交流电源上，“3 V，6 W”的灯泡恰好正常发光，电阻R2=18.5 Ω，电压表V为理想电表。下列推断正确的是（ ）

A. 交变电流的频率为100 Hz B. 穿过铁芯的磁通量的最大变化率为 Wb/s

C. R1消耗的功率是8 W D. 电压表V的示数为44 V

【题目】如图所示，两条平行的光滑金属导轨相距L=1 m，金属导轨由倾斜与水平两部分组成，倾斜部分与水平方向的夹角为θ=37°，整个装置处在竖直向上的匀强磁场中。金属棒EF和MN的质量均为m=0.2 kg，电阻均为R=2 Ω。EF置于水平导轨上，MN置于倾斜导轨上，两根金属棒均与导轨垂直且接触良好。现在外力作用下使EF棒以速度v0=4 m/s向左匀速运动，MN棒恰能在倾斜导轨上保持静止状态。倾斜导轨上端接一阻值也为R的定值电阻。重力加速度g=10 m/s2。

（1）求磁感应强度B的大小；

（2）若将EF棒固定不动，将MN棒由静止释放，MN棒沿斜面下滑距离d=5 m时达到稳定速度，求此过程中通过MN棒的电荷量；

（3）在（2）过程中，整个电路中产生的焦耳热。

【题目】（10分）如图所示，静止的气缸内封闭了一定质量的气体，水平轻杆一端固定在墙壁上，另一端与气缸内的活塞相连。已知大气压强为1.0×105Pa，气缸的质量为50kg，活塞质量不计，其横截面积为0.01m2，气缸与地面间的最大静摩擦力为气缸重力的0.4倍，活塞与气缸之间的摩擦可忽略。开始时被封闭气体压强为1.0×105Pa、温度为27℃，试求：

（1）缓慢升高气体温度，气缸恰好开始向左运动时气体的压强P和温度t；

（2）某同学认为封闭气体的温度只有在27C到（1）问中t之间，才能保证气缸静止不动，你是否同意他的观点？若同意，请说明理由；若不同意，计算出正确的结果。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网