题目内容
如图所示,在以O为圆心、半径为R的圆形区域内,有一个水平方向的匀强磁场,磁场的磁感应强度大小为B,方向垂直纸面向外。竖直平行正对放置的两金属板A、K连在电压可调的电路中。S1、S2为A、K板上的两个小孔,且S1、S2和O在同一直线上,另有一水平放置的足够大的荧光屏D,O点到荧光屏的距离为h。比荷(电荷量与质量之比)为k的带正电的粒子由S1进入电场后,通过S2射向磁场中心,通过磁场后打在荧光屏D上。粒子进入电场的初速度及其所受重力均可忽略不计。
(1)请分段描述粒子自S1到荧光屏D的运动情况;
(2)求粒子垂直打到荧光屏上P点时速度的大小;
(3)移动滑片P,使粒子打在荧光屏上Q点,PQ=33h(如图19所示),求此时A、K两极板间的电压。
解:(1)粒子在电场中自S1至S2做匀加速直线运动;自S2至进入磁场前做匀速直线运动;进入磁场后做匀速圆周运动;离开磁场至荧光屏做匀速直线运动。

(2)设粒子的质量为m,电荷量为q,垂直打在荧光屏上的P点时的速度为v1,粒子垂直打在荧光屏上,说明粒子在磁场中的运动是四分之一圆周,运动半径r1=R,
根据牛顿第二定律Bqv1=m![]() ,依题意:
,依题意:
k=q/m
解得v1=BkR。

(3)设粒子在磁场中运动轨道半径为r2,偏转角为2θ,粒子射出磁场时的方向与竖直方向夹角为α,粒子打到Q点时的轨迹如图所示,由几何关系可知
tanα=![]() ,α=30°,θ=30°
,α=30°,θ=30°
tanθ=![]() 解得r2=
解得r2=![]() R
R
设此时A、K两极板间的电压为U,粒子离开S2时的速度为v2,根据牛顿第二定律
Bqv2=m![]()
根据动能定理有qU=![]() mv22
mv22
解得U=![]() kB2R2。
kB2R2。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
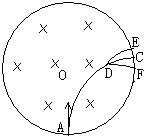 (2004?惠州一模)如图所示,在一个半径为R的圆形区域内存在着匀强磁场,磁场方向垂直于圆面向里,一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内,粒子将做圆周运动到达磁场边界的C点,但在粒子经过D点时,恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子,关于这个新粒子的运动情况,以下判断正确的是( )
(2004?惠州一模)如图所示,在一个半径为R的圆形区域内存在着匀强磁场,磁场方向垂直于圆面向里,一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内,粒子将做圆周运动到达磁场边界的C点,但在粒子经过D点时,恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子,关于这个新粒子的运动情况,以下判断正确的是( ) 如图所示,在圆心O处固定一正点电荷,现从P点以相同的速率发射两个检验电荷a、b,分别沿PM、PN运动到M、N两点,M、N都在以O为圆心的圆上.若检验电荷a、b的质量、电荷量均相等,则下列判断正确的是( )
如图所示,在圆心O处固定一正点电荷,现从P点以相同的速率发射两个检验电荷a、b,分别沿PM、PN运动到M、N两点,M、N都在以O为圆心的圆上.若检验电荷a、b的质量、电荷量均相等,则下列判断正确的是( ) 如图所示,在圆心O处固定一正点电荷,两个质量和电量均相同的检验电荷a、b从P点以相同的速率,分别沿PN、PM运动到N、M(均在以O为圆心的圆上),下列说法正确的是( )
如图所示,在圆心O处固定一正点电荷,两个质量和电量均相同的检验电荷a、b从P点以相同的速率,分别沿PN、PM运动到N、M(均在以O为圆心的圆上),下列说法正确的是( )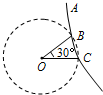 如图所示,在点O置于一个正点电荷,在过点O的竖直平面内的点A处,自由释放一个带正电的小球,小球的质量为m,带电量为q,小球落下的轨迹如图中实线所示,它与以O为圆心,R为半径的圆相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC高度为h,若小球过B点时的速度为v,则( )
如图所示,在点O置于一个正点电荷,在过点O的竖直平面内的点A处,自由释放一个带正电的小球,小球的质量为m,带电量为q,小球落下的轨迹如图中实线所示,它与以O为圆心,R为半径的圆相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC高度为h,若小球过B点时的速度为v,则( )