题目内容
【题目】(9分)有一个高度为h=0.6m的金属容器放置在水平地面上,容器内有温度为t1=27 ℃的空气,容器左侧壁有一阀门距底面高度为h1=0.3m,阀门细管直径忽略不计.容器内有一质量为m=5.0 kg的水平活塞,横截面积为S=20 cm2,活塞与容器壁紧密接触又可自由活动,不计摩擦,现打开阀门,让活塞下降直至静止并处于稳定状态。外界大气压强为p0=1.0×105 Pa.阀门打开时,容器内气体压强与大气压相等,g取10 m/s2。求:
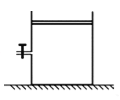
(1)若不考虑气体温度变化,则活塞静止时距容器底部的高度h2;
(2)活塞静止后关闭阀门,对气体加热使容器内气体温度升高到327 ℃,求此时活塞距容器底部的高度h3。
【答案】(1)0.24 m (2)0.48 m
【解析】
试题分析:(1)活塞经阀门细管时,容器内气体的压强为p1=1.0×105 Pa
活塞静止时,气体的压强为p2=p0+mg/S=1.25×105 Pa
容器内气体的体积为V1=20×10-4×0.3 m3=6.0×10-4 m3
活塞静止时,气体的体积为V2=h2×20×10-4 m3
根据玻意耳定律p1V1=p2V2
代入数据得h2=![]() =0.24m
=0.24m
(2)活塞静止后关闭阀门,此时气体的压强为
p3=p2=1.25×105 Pa
等压变化:T2=T1=300 K,T3=600 K
V2=h2S=4.8×10-4 m3,V3=h3×20×10-4 m3
根据盖·吕萨克定律![]()
代入数据得h3=0.48 m

练习册系列答案
相关题目