题目内容
6.地球的同步卫星距地面高H约为地球半径R的5倍,同步卫星正下方的地面上有一静止的物体A,则同步卫星与物体A的向心加速度之比是多少?若给物体A以适当的绕行速度,使A成为近地卫星,则同步卫星与近地卫星的向心加速度之比是多少?分析 (1)同步卫星与物体A周期相等,根据圆周运动公式求解.
(2)对于卫星A和同步卫星均绕地球做匀速圆周运动,根据万有引力提供向心力得出加速度关系
解答 解:地面上物体A与同步卫星有相同的角速度,由${a_n}={ω^2}r$得:$\frac{a_n}{a_A}=\frac{r_n}{r_A}=6$:1
又:由$G\frac{Mm}{r^2}=m{a_n}$得:${a_n}=G\frac{M}{r^2}$所以:$\frac{a_n}{a_n^'}=\frac{{r_n^{'2}}}{r_n^2}=\frac{1}{36}$.
答:同步卫星与物体A的向心加速度之比是6:1,若给物体A以适当的绕行速度,使A成为近地卫星,则同步卫星与近地卫星的向心加速度之比,1:36
点评 解决本题的关键掌握同步卫星的特点,以及掌握万有引力提供向心力这一理论,并能熟练运用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.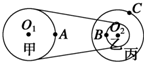 如图所示的皮带传动装置中,甲轮的轴和塔轮丙和乙的轴均为水平轴,其中,甲、丙两轮半径相等,乙轮半径是丙轮半径的一半.A、B、C三点分别是甲、乙、丙三轮的边缘点,若传动中皮带不打滑,则( )
如图所示的皮带传动装置中,甲轮的轴和塔轮丙和乙的轴均为水平轴,其中,甲、丙两轮半径相等,乙轮半径是丙轮半径的一半.A、B、C三点分别是甲、乙、丙三轮的边缘点,若传动中皮带不打滑,则( )
 如图所示的皮带传动装置中,甲轮的轴和塔轮丙和乙的轴均为水平轴,其中,甲、丙两轮半径相等,乙轮半径是丙轮半径的一半.A、B、C三点分别是甲、乙、丙三轮的边缘点,若传动中皮带不打滑,则( )
如图所示的皮带传动装置中,甲轮的轴和塔轮丙和乙的轴均为水平轴,其中,甲、丙两轮半径相等,乙轮半径是丙轮半径的一半.A、B、C三点分别是甲、乙、丙三轮的边缘点,若传动中皮带不打滑,则( )| A. | A、B两点的线速度大小之比为2:1 | |
| B. | B、C两点的角速度大小之比为1:2 | |
| C. | A、B两点的向心加速度大小之比为2:1 | |
| D. | A、C两点的向心加速度大小之比为1:4 |
17.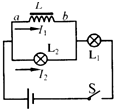 如图所示电路为演示自感现象的实验电路.若闭合开关S,电流达到稳定后通过线圈L的电流为I1,通过小灯泡L2的电流为I2,小灯泡L2处于正常发光状态.以下说法正确的是( )
如图所示电路为演示自感现象的实验电路.若闭合开关S,电流达到稳定后通过线圈L的电流为I1,通过小灯泡L2的电流为I2,小灯泡L2处于正常发光状态.以下说法正确的是( )
 如图所示电路为演示自感现象的实验电路.若闭合开关S,电流达到稳定后通过线圈L的电流为I1,通过小灯泡L2的电流为I2,小灯泡L2处于正常发光状态.以下说法正确的是( )
如图所示电路为演示自感现象的实验电路.若闭合开关S,电流达到稳定后通过线圈L的电流为I1,通过小灯泡L2的电流为I2,小灯泡L2处于正常发光状态.以下说法正确的是( )| A. | S闭合后,L2灯缓慢变亮,L1灯立即亮 | |
| B. | S断开后,L1灯L2灯都将延迟熄灭 | |
| C. | S闭合后,通过线圈L的电流由零逐渐增大到I1 | |
| D. | S断开后,小灯泡L2中的电流由I2逐渐减为零,方向不变 |
14.波速均为v=2m/s的甲、乙两列简谐横波都沿x轴正方向传播,某时刻波的图象分别如图所示,其中P、Q处的质点均处于波峰.关于这两列波,下列说法正确的是( )
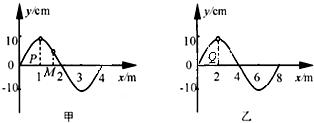

| A. | 甲波中的P处质点比M处质点先回平衡位置 | |
| B. | 从图示的时刻开始,经过1.0s,P质点通过的位移为2m | |
| C. | 此时刻,M点的运动方向沿x轴正方向 | |
| D. | 从图示的时刻开始,P处质点比Q处质点先回平衡位置 | |
| E. | 如果这两列波相遇不可能产生稳定的干涉图样 |
1.关于物质波,以下观点不正确的是( )
| A. | 只要是运动着的物体,不论是宏观物体还是微观粒子,都有相应的波与之对应,这就是物质波 | |
| B. | 只有运动着的微观粒子才有物质波,对于宏观物体,不论其是否运动,都没有相对应的物质波 | |
| C. | 由于宏观物体的德布罗意波长太小,所以无法观察到它们的波动性 | |
| D. | 电子束照射到金属晶体上得到了电子束的衍射图样,从而证实了德布罗意的假设是正确的 |
11.小明感到“大地扑面而来”,他所选择的参考系是( )
| A. | 自己 | B. | 塔台 | C. | 地面 | D. | 天空 |
18.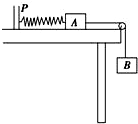 如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,弹簧处于水平状态;物体A置于光滑水平桌面上,A右端水平连接一细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让系统处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度(假设此过程中B未着地).已知弹簧的劲度系数为k,A、B两物体的质量均为m,物体A始终处在水平桌面上,不计绳的伸长,重力加速度为g.下列说法正确的是( )
如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,弹簧处于水平状态;物体A置于光滑水平桌面上,A右端水平连接一细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让系统处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度(假设此过程中B未着地).已知弹簧的劲度系数为k,A、B两物体的质量均为m,物体A始终处在水平桌面上,不计绳的伸长,重力加速度为g.下列说法正确的是( )
 如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,弹簧处于水平状态;物体A置于光滑水平桌面上,A右端水平连接一细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让系统处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度(假设此过程中B未着地).已知弹簧的劲度系数为k,A、B两物体的质量均为m,物体A始终处在水平桌面上,不计绳的伸长,重力加速度为g.下列说法正确的是( )
如图所示,轻质弹簧的一端与固定的竖直板P连接,另一端与物体A相连,弹簧处于水平状态;物体A置于光滑水平桌面上,A右端水平连接一细线,细线绕过光滑的定滑轮与物体B相连.开始时托住B,让系统处于静止状态且细线恰好伸直,然后由静止释放B,直至B获得最大速度(假设此过程中B未着地).已知弹簧的劲度系数为k,A、B两物体的质量均为m,物体A始终处在水平桌面上,不计绳的伸长,重力加速度为g.下列说法正确的是( )| A. | 物体A与物体B组成的系统机械能守恒 | |
| B. | 当物体B获得最大速度时,弹簧伸长量为$\frac{2mg}{k}$ | |
| C. | 当物体B获得最大速度时,若弹簧的弹性势能增加量为$\frac{{{m^2}{g^2}}}{2k}$,则物体A的速度大小为$g\sqrt{\frac{m}{2k}}$ | |
| D. | 此过程中B物体机械能的减少量大于弹簧弹性势能的增加量 |
15. 如图所示是杂技演员在表演“水流星”的节目,盛水的杯子经过最高点杯口向下时水也不洒出来.对于杯子经过最高点时水的受力情况,下列说法正确的是( )
如图所示是杂技演员在表演“水流星”的节目,盛水的杯子经过最高点杯口向下时水也不洒出来.对于杯子经过最高点时水的受力情况,下列说法正确的是( )
 如图所示是杂技演员在表演“水流星”的节目,盛水的杯子经过最高点杯口向下时水也不洒出来.对于杯子经过最高点时水的受力情况,下列说法正确的是( )
如图所示是杂技演员在表演“水流星”的节目,盛水的杯子经过最高点杯口向下时水也不洒出来.对于杯子经过最高点时水的受力情况,下列说法正确的是( )| A. | 杯底对水的作用力可能为零 | |
| B. | 水受平衡力的作用,合力为零 | |
| C. | 由于水做圆周运动,因此必然受到重力和向心力的作用 | |
| D. | 水处于失重状态,不受重力的作用 |
16.火车在平直轨道上匀速行驶,门窗紧闭的车厢内有一人向上跳起,发现仍落回原处的原因是( )
| A. | 人跳起后,车厢内空气给他以向前的推力,带着他随同火车一起向前运动 | |
| B. | 人跳起瞬间,车厢地板给他一向前的推力,推动他随同火车一起向前运动 | |
| C. | 人跳起后,车在继续向前运动,所以人落下后必定偏后一些,只是由于时间很短,偏后的距离不明显? | |
| D. | 人跳起后直到落地,在水平方向上始终和车具有相同的速度 |