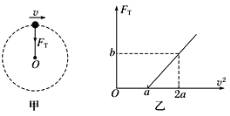
题目内容
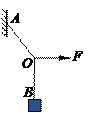
【题目】图是离心轨道演示仪结构示意图。光滑弧形轨道下端与半径为R的光滑圆轨道相接,整个轨道位于竖直平面内。质量为m的小球从弧形轨道上的A点由静止滑下,进入圆轨道后沿圆轨道运动,若小球通过圆轨道的最高点时对轨道的压力与重力等大。小球可视为质点,重力加速度为g,不计空气阻力。求:
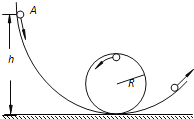
(1)小球运动到圆轨道的最高点时速度的大小;
(2)小球开始下滑的初始位置A点距水平面的竖直高度h;
(3)小球从更高的位置释放,小球运动到圆轨道的最低点和最高点时对轨道的压力之差。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)小球经过最高点,轨道的压力N=mg, 依据牛顿第三定律可知小球对轨道压力为mg,由牛顿第二定律有:mg+mg=![]()
解得 v=![]()
(2)小球自A点下滑至圆轨道最高点的过程,依据动能定理有
![]()
解得 h=![]()
(3)设小球从更高的位置释放运动到最低点时的速度为v1,受轨道的压力为N1;运动到最高点时的速度为v2,受轨道的压力为N2;依据牛顿第二定律有
![]()
![]()
小球由最低点运动到最高点的过程,依据动能定理有:![]()
得压力差 ![]()

练习册系列答案
相关题目