��Ŀ����
����Ŀ��Ϊ����֤��ײ�еĶ����غ�ͼ�������С�����ײ�Ƿ�Ϊ������ײ����ײ������û�л�е����ʧ����ijͬѧѡȡ�����������ͬ���������ȵ�С������������������ʵ�飺
������ƽ�������С��������ֱ�Ϊm1��m2 �� ��m1��m2 ��
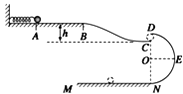
�ڰ�����ͼ��ʾ����������װ��ʵ��װ�ã���б��AB�̶������ߣ�ʹ�۵�ĩ�˵������ˮƽ����һб��BC������б��ĩ�ˣ�
���Ȳ���С��m2 �� ��С��m1��б�۶���A���ɾ�ֹ��ʼ���£�����С����б���ϵ����λ�ã�
�ܽ�С��m2����б��ǰ�˱�Ե������С��m1��б�۶���A�����£�ʹ���Ƿ�����ײ������С��m1��С��m2��б���ϵ����λ�ã�
���ú��̶ȳ������������λ�õ�б��ĩ�˵�B�ľ��룮ͼ��D��E��F���Ǹ�ͬѧ���µ�С����б���ϵļ������λ�ã���B��ľ���ֱ�ΪLD��LE��LF ��
���ݸ�ͬѧ��ʵ�飬�ش��������⣺
��1��С��m1��m2������ײ��m1�������ͼ�е��㣬m2�������ͼ�е��㣮
��2���ò�õ�����������ʾ��ֻҪ�����ϵʽ �� ��˵����ײ�ж������غ�ģ�
��3���ò�õ�����������ʾ��ֻҪ�������ϵʽ �� ��˵����С�����ײ�ǵ�����ײ��
���𰸡�
��1��D,F
��2��![]()
��3��m1LE=m1LD+m2LF
���������⣺��1��С��m1��С��m2��ײ��С��m2���ٶ�����С��m1���ٶȼ�С������ƽ���˶���������ײ��m1�����ص���D�㣬m2�����ص���F�㣻��2����ײǰ��С��m1����ͼ�е�E�㣬����ˮƽ���ٶ�Ϊv1��С��m1��m2������ײ��m1�������ͼ�е�D�㣬����ˮƽ���ٶ�Ϊv1�䣬m2�������ͼ�е�F�㣬����ˮƽ���ٶ�Ϊv2�� ��б��BC��ˮƽ������Ϊ����
��ƽ���˶����ɵã� ![]() ��LDcos��=v��1t
��LDcos��=v��1t
��ã� ![]()
ͬ���ɽ�ã� ![]() ��
�� ![]()
����ֻҪ����m1v1=m2v2+m1v��1���� ![]() ��˵��������ײ�����ж����غ㣻��3������С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ����Ҫ�����ϵʽ
��˵��������ײ�����ж����غ㣻��3������С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ����Ҫ�����ϵʽ
![]() m1v12=
m1v12= ![]() m1v��12+
m1v��12+ ![]() m2v2
m2v2
��m1LE=m1LD+m2LF
�ʴ�ΪΪ����1��D��F��2�� ![]() ��3��m1LE=m1LD+m2LF
��3��m1LE=m1LD+m2LF
��1������С����ײ֮����ƽ���˶�����ˮƽ��������ٶȸ���ƽ���˶����ɽ����жϣ�
��2������ƽ���˶����������ײǰ��С��m1��С��m2���ٶȣ���ʾ�������ı���ʽ������⣻
��3����С�����ײ�ǵ�����ײ������ײǰ���е��û����ʧ��

 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�