题目内容
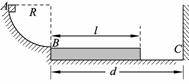
如图所示，放置在光滑水平面上的长木板，其上表面与左侧竖直平面内的
光滑圆弧轨道底端B相切，木板长度l=1.2 m，质量M=2 kg。与圆弧轨道末端相距d=1.6 m的C处有一竖直墙。质量m=2 kg的小滑块从圆弧轨道顶端A由静止滑下，离开B后在木板上滑行。已知圆弧轨道半径R=0.2 m，滑块与木板间的动摩擦因数μ=0.2，木板与左右两侧发生碰撞后能原速率返回。(g取10 m/s2)试求
(1) 滑块滑至圆弧轨道底端B时对轨道的压力N
(2) 滑块最终位置与竖直墙间的距离S
(3) 整个过程中产生的热量Q
(1) 滑块下滑过程，由机械能守恒定律得
mgR=
mv2……………………………………………………………………（2分）
v=
m/s=2 m/s
由向心力公式得
N′-mg=m
…………………………………………………………………………（1分）
解得N′=mg+m=2×10+2×
N=60 N
根据牛顿第三定律，滑块对轨道的压力N=60 N…………………………………（1分）
(2) 由牛顿第二定律，滑块做减速运动的加速度大小为
a1=μg=0.2×10 m/s2=2 m/s2…………………………………………………………（1分）
木板加速运动的加速度大小为
a2=
=0.2×10 m/s2=2 m/s2…………………………………………………（1分）
滑块向右滑动至与木板速度相同过程所用时间设为t，则有
v-a1t=a2t
解得t=0.5 s
共同运动速度v′=a2t=1 m/s
这段时间内滑块位移大小s1=vt-a1t2=2×0.5-×2×0.52 m=0.75 m
木板位移大小s2=a2t2=×2×0.52 m=0.25 m
因为S2＜d-l，所以滑块相对木板滑行0.5 m后，与木板共同向右做匀速运动，直到木板与墙发生碰撞。………………………………………………………………（3分）
设碰撞后至滑块与木板达到共同速度时间为t′，则有
v′-a1t′=-v′+a2t′
解得t′=0.5 s
滑块和木板与墙碰撞后向左运动的最终共同速度为v″=v′-a1t′=0
这段时间内滑块向右运动位移大小为S1′=v′t′=0.25 m
木板向左运动位移大小为S2′=v′t′=0.25 m
由于S1′+S2′＜l-(S1-S2)，滑块最终静止在木板上……………………………（3分）
由几何关系判断，滑块最终位置离墙的距离为S=l-(s1-s2)-s′1=0.45 m………………
……………………………………………………………………………………（1分）
(3) 由功能关系，整个过程中产生的热量为
Q=mgR=2×10×0.2 J=4 J……………………………………………………………（3分）
如图所示是放置在竖直平面内的游戏滑轨，有一质量m=2kg的小球穿在轨道上．滑轨由四部分粗细均匀的滑杆组成；水平轨道AB；与水平面间的成夹角θ=370且长L=6m的倾斜直轨道CD；半径R=1m的圆弧轨道APC；半径R=3m的圆弧轨道BQED．直轨道与圆弧轨道相切，切点分别为A、B、D、C，E为最低点．倾斜轨道CD与小球间的动摩擦因数
如图所示是放置在竖直平面内的游戏滑轨，有一质量m=2kg的小球穿在轨道上．滑轨由四部分粗细均匀的滑杆组成：水平直轨道AB；倾斜直轨道CD，长L=6m，与水平面间的夹角θ=370；半径R1=1m的圆弧轨道APC；半径R2=3m的圆弧轨道BQED．直轨道与圆弧轨道相切，切点分别为A、B、D、C，E为最低点．倾斜直轨道CD与小球间的动摩擦因数为μ=5/32，其余部分均为光滑轨道，取g=10m/s2，sin37°=0.6，cos37°=0.8．现让小球从AB的正中央以初速度V0=10m/s开始向左运动，问：
如图所示是固定在光滑水平地面上的两条光滑长直导轨（俯视图）．导轨内放置一个木质滑块A，滑块A的左半部是半径为R的半圆柱形光滑凹槽，木质滑块的宽度为2R．现有半径r（r＜＜R）的金属小球沿水平面以初速度v0冲向滑块，从滑块的一侧半圆形槽口边缘进入．已知金属小球的质量为m，木质滑块A的质量为3m，整个运动过程中无机械能损失．求：
（2010?上海模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为θ=37°．现有一质量为m=1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ=